Метод секущих для решения нелинейных уравнений

Метод секущих берёт начало от метода касательных Ньютона, то есть вычисляется по той же формуле:

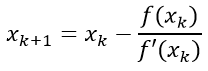
только производная заменяется на формулу разностей:

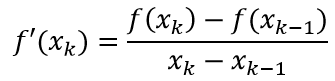
тогда формула для вычисления с помощью метода секущих примет вид:

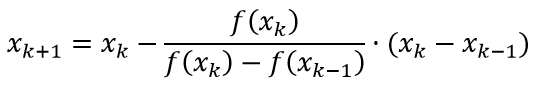
при условии

|x_k+1–x_k|<ε

ε – абсолютная погрешность вычисления корня уравнения.

---

Пример
Численным методом найдите корни нелинейного уравнения

(x)=Ln|x|-0.05e^x

с помощью метода секущих с точностью 0,0001 на промежутке x∈[0,6;1]
Решение

Построим график исходной функции

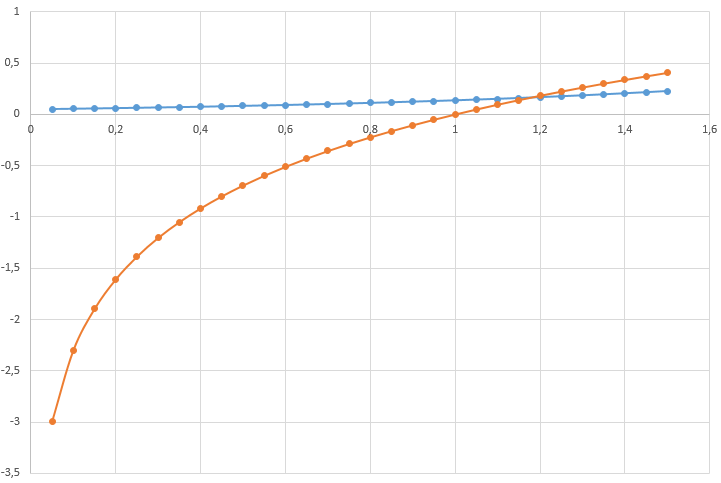
Зададим два начальных приближения, пусть это будут точки x₀=0,6 и x₁=1 по формуле:

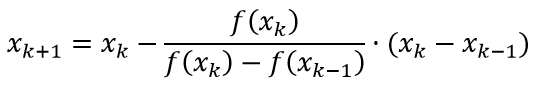
Найдем последовательно корни и запишем их в таблицу ниже.

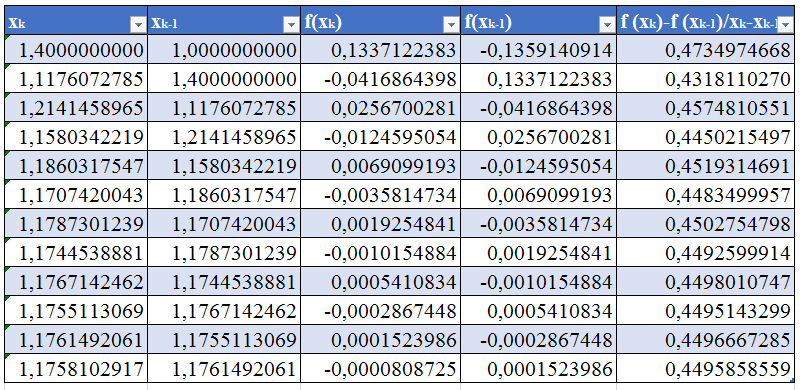
Из таблицы корень уравнения равен:

x=1,1758102917