Решение уравнений методом касательных Ньютона

Метод касательных Ньютона — это итерационный метод поиска корня и относится к численному методу решения нелинейного уравнения.
Формула касательных (Ньютона):

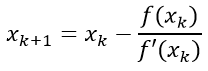
Условие достаточной сходимости метода Ньютона:

f(x)·f ′′(x)>0

при этом

|x_k+1–x_k|<ε

ε – оценка точности вычисления корня уравнения.
Рассмотрим данный метод на примере решения нелинейного уравнения.

К модифицированному методу касательных Ньютона относится метод касательных.

---

Пример
Найдите корни уравнения

f(x)=Ln|x|-0.05e^x

с помощью метода касательных Ньютона с точностью 0,0001
Решение
Найдем производную уравнения нелинейной функции

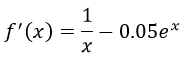
Построим график уравнений

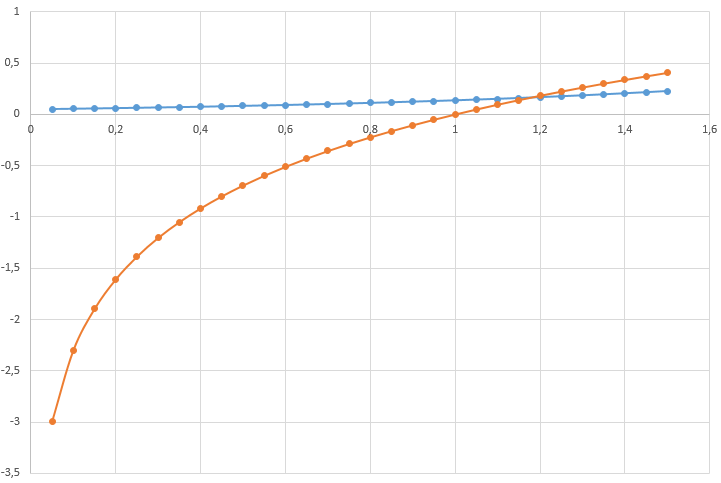
Как видно из графиков функций, корень уравнения приблизительно находится на промежутке x∈[1,0;1,4]
В качестве начального приближенного значения возьмём значение на начале данного отрезка, то есть 1.
Для поиска корней нелинейного уравнения воспользуемся формулой касательных (Ньютона):

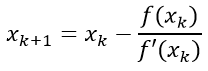
Для упрощения вычислений воспользуемся таблицей

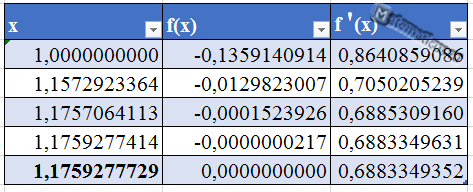
Итак, корень уравнения равен:

x=1,17592777285712