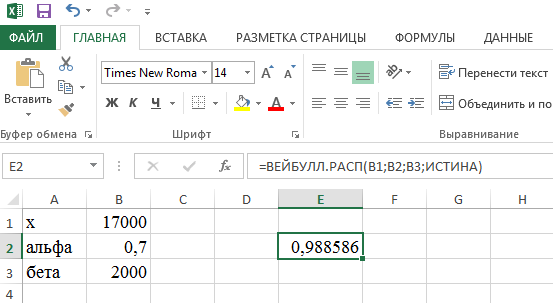
В Excel распределение Вейбулла вычисляются по общей формуле:
ВЕЙБУЛЛ.РАСП(x;альфа;бета;интегральная)
Так как интегральная составляющая в данной формуле имеет два значения: ИСТИНА или ЛОЖЬ, то формулу запишем в виде:
Формула для интегральной функции распределения Вейбулла:
ВЕЙБУЛЛ.РАСП(x;альфа;бета;ИСТИНА)
Аналитическое выражение для интегральной функции:
$F(x,\alpha ,\beta )=1-e^{-(\frac{x}{\beta })^{\alpha }}$
Формула для функции плотности распределения Вейбулла:
ВЕЙБУЛЛ.РАСП(x;альфа;бета;ЛОЖЬ)
Аналитическое выражение для функции плотности распределения Вейбулла:
$f(x,\alpha ,\beta )=\frac{\alpha }{\beta }\frac{x}{\beta }^{\alpha -1}e^{-(\frac{x}{\beta })^{\alpha }}$
Пример
Время до отказа ЭВМ подчиняется распределению Вейбулла со следующими параметрами: α=0.7 и β=2000 часов.
Какова вероятность того, что ЭВМ прослужит более 17000 часов?
Решение
Решим задачу в Excel