Движение тела брошенного под углом к горизонту

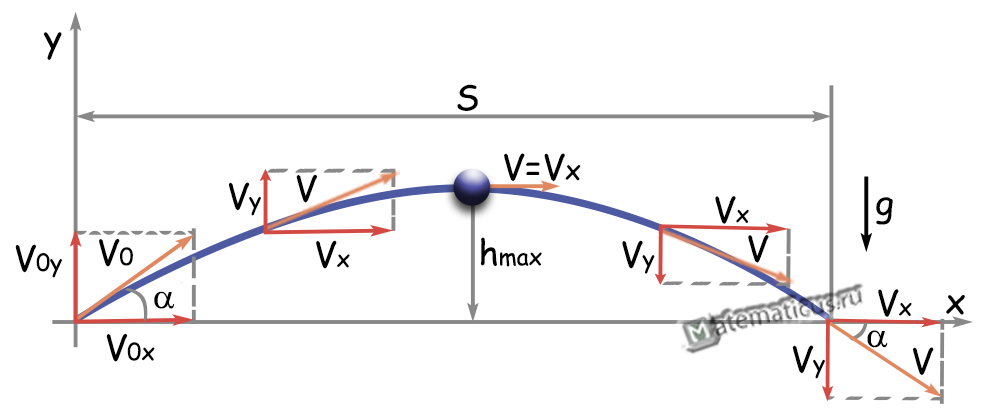
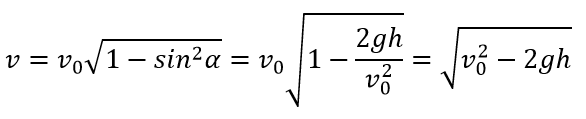Движение тела брошенного под углом к горизонту движется по параболе. Максимальная дальность полета тела брошенного под углом к горизонту достигается при угле бросания 45⁰. Основоположником данной задачи динамики является Галилео Галилей.

$x\left( t \right) = t{v_0}cos\alpha $

$y\left( t \right) = t{v_0}sin\alpha — \frac{{g{t^2}}}{2}$

$y = xtg\alpha — {x^2}\frac{g}{{v_0^2co{s^2}\alpha }}$

Здесь, по оси OX уравнение имеет вид:

V_x=V_0x

V_0x=V₀cosα

по оси OY:

V_y=V_0y−gt

V_0y=V₀sinα

Скорость тела в любой точке определяется:

$v = \sqrt {v_x^2 + v_y^2} $

Формула для определения время полета из уравнения 0=V₀sinα−gt_п:

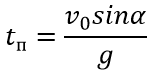
Формула для определения максимальной высоты полета из уравнения:

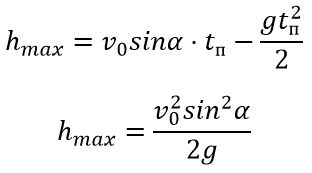
Общее время движения вычисляется по формуле:

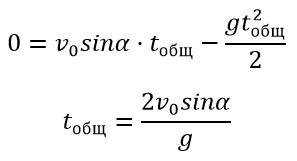
Время падения вычисляется по формуле:

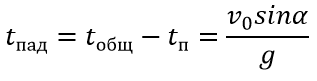
Формула дальности броска:

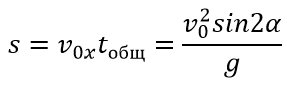
Скорость в высшей точки траектории имеет математическое выражение: