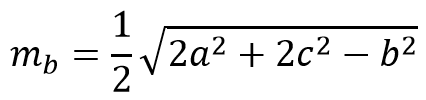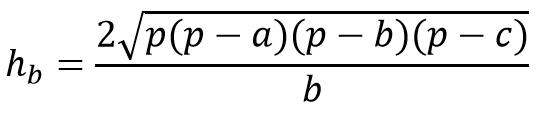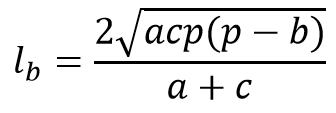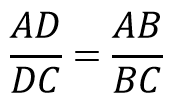Медиана треугольника
Медиана — это отрезок BM, соединяющий вершину треугольника B и середину противоположной стороны AM=MC. Из этого следует вывод, что медиана делит стороны пополам.
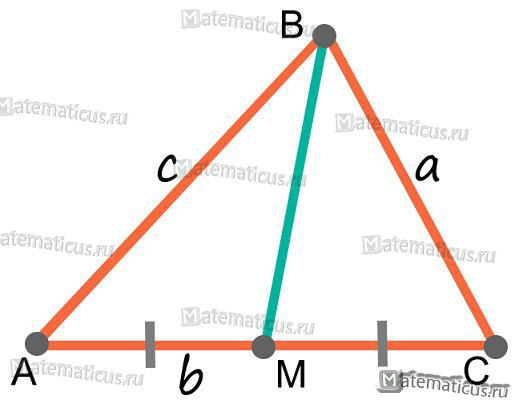
BM — медиана
Формула длины медианы треугольника:
Свойство медианы треугольника
В треугольнике три медианы пересекаются в одной точке и делятся в отношении 2:1.
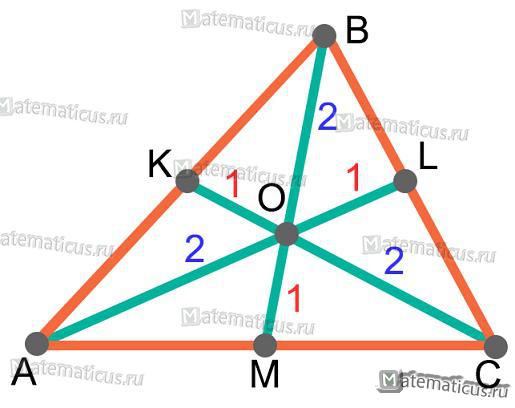
BM, KC, AL — медианы треугольника
Здесь точка O — центр тяжести треугольника
Высота треугольника
Высота — это перпендикуляр, опущенный из вершины треугольника B к основанию AC.
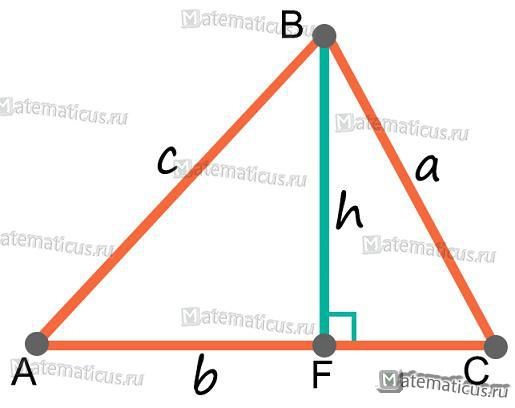
BF — высота
Формула длины высоты треугольника:
где
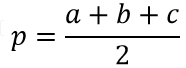
Биссектриса треугольника
Биссектрисой треугольника называется отрезок BD, который соединяет вершину B треугольника с точкой противоположной стороны и лежит на луче, разделяющей данный угол пополам. По сути, биссектриса делит угол пополам, ∠ABD=∠DBC
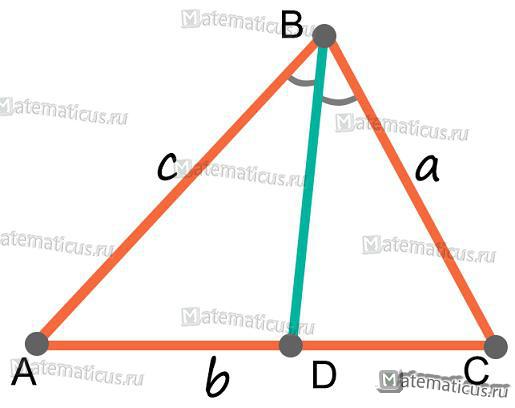
BD — биссектриса
Формула длины биссектрисы треугольника:
где
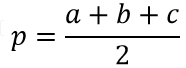
Свойство биссектрисы треугольника
- AD относится к DC, как AB к BC
2. В треугольнике три биссектрисы пересекаются в одной точке и эта точка является центром вписанной окружности в треугольник.
В треугольнике медианы пересекаются в одной точке, это также относится и к высоте и биссектрисе.