Окружность — это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости на заданное расстояние (рисунок 1).
Круг — часть плоскости, которая ограниченна окружностью (рисунок 1).
Другое понятие круга.
Круг — это часть плоскости, которая лежит внутри окружности, вместе с самой окружностью (рисунок 1).
Рисунок 1
Радиус r — это любой отрезок, соединяющий центр окружности и точку окружности. На рисунке 2 это отрезок OC.
Также радиус от лат. называли спицу в колесе.
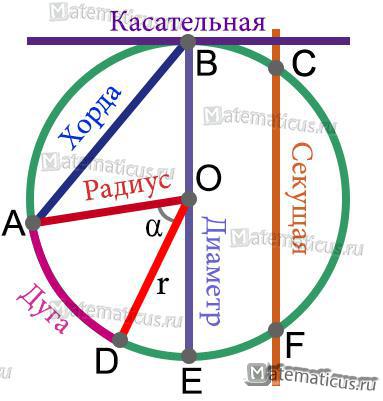
Рисунок 2
Хорда — это отрезок AB, соединяющий две точки окружности (рисунок 2).
Диаметр — это хорда BE, проходящая через цент окружности (рисунок 2).
Если на окружности взять две точки, то они разобьют окружность на две части (рисунок 2). Каждая из этих кривых называется дугой окружности, а точки A и D — концы этих дуг.
Дуга обозначается как ∪ AD (рисунок 2).
Длина дуги окружности ∪AB (рисунок 3) находится по формуле:
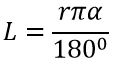
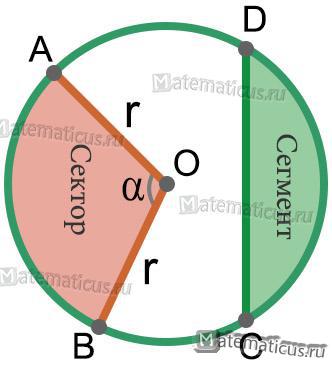
Рисунок 3
Сектор круга — это часть плоскости, ограниченная двумя радиусами и его дугой (рисунок 3).
Площадь сектора, формула:
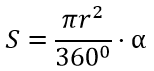
Сегмент круга — это часть плоскости, ограниченная хордой и дугой (рисунок 3).
Площадь сектора окружности, формула:
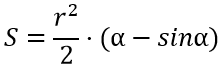
Касательной называется прямая a, имеющая с окружностью только одну общую точку A (рисунок 5).
Формула для расчета длины окружности через радиус:
L=2πr
Формула для расчета длины окружности через диаметр:
L=2πd
Формула для определения площади круга через радиус:
S=πR2
Формула для определения площади круга через диаметр:
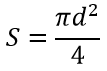
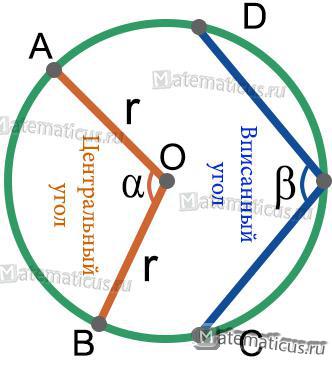
Рисунок 4
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Формула для определения длины хорды ∪ AB через радиус и центральный угол ∠BOA:
AB=2rsin α/2
Формула для определения длины хорды через радиус и вписанный угол ∠CED:
CD=2rsinα
Свойства касательной к окружности
Одно из свойств касательной к окружности (рисунок 5) заключается в том, что касательная a к окружности перпендикулярна ее радиусу OA. Из этого вытекает аналогичное свойство, т.е. касательная , проходящая через точку касания с окружностью, перпендикулярна диаметру.
OA⊥a
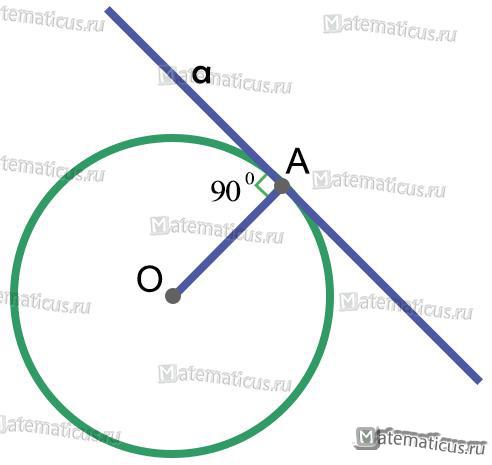
Рисунок 5
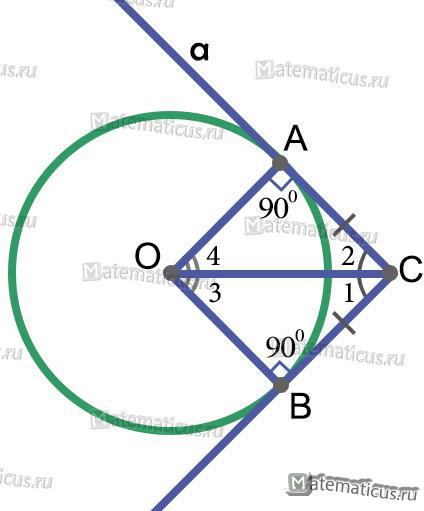
Рисунок 6
CA, CB – касательные
A, B – точки касания
CA = CB
В соответствии с рисунком 6, получаем свойство
∠1 = ∠2; ∠3 = ∠4
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Свойства секущей окружности
Секущая окружности — это прямая BE, имеющая с окружностью две общие точки (рисунок 7).
В соответствии с рисунком 7, получаем свойство
BA2=BF⋅BD
BA2=BE⋅BC
где AB — касательная
BE, BF — секущие
Из этого свойства вытекает следующее свойство, произведения отрезков секущих, проведенных из одной точки равны:
BF⋅BD=BE⋅BC
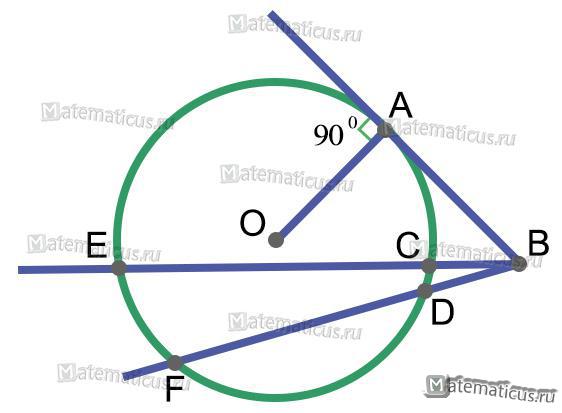
Рисунок 7
Свойства окружности
- Диаметр окружности равен сумме двух радиусов, то есть
d =r+r=2·r
- Через три точки, не лежащих на одной прямой, можно построить только единственную окружность.
- Если взять все замкнутые кривые с одинаковой длиной, то окружность имеет максимальную величину площади.
-
Кратчайшее расстояние от центра окружности к секущей или хорде всегда меньше величины радиуса.
- Если две окружности соприкасаются внешне или внутренне в одной точке, то точка касания и центры этих окружностей лежат на одной прямой.
Свойства углов окружности
На рисунке 8
∪ CB — дуга окружности
∠COB — центральный угол
∠CAB — вписанный угол
Получаем следующее тождество:
∠CAB = ∠COB/2
при этом длина дуги окружности ∪ CB должна быть меньше длины полуокружности.
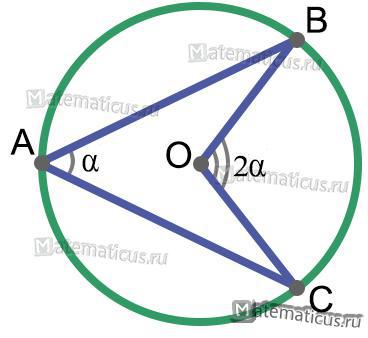
Рисунок 8
Вписанные углы, опирающиеся на одну и ту же дугу, равны (рисунок 9).
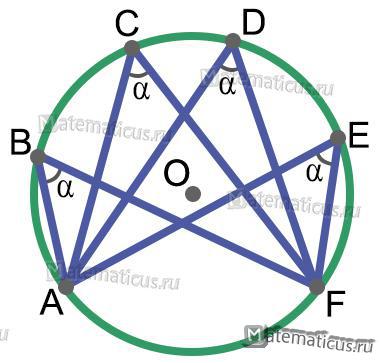
Рисунок 9
Вписанный угол, опирающийся на полуокружность – прямой (рисунок 10).
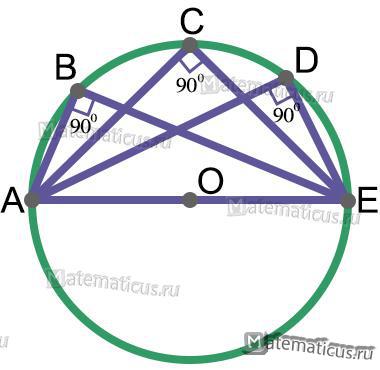
Рисунок 10
Свойство хорд окружности
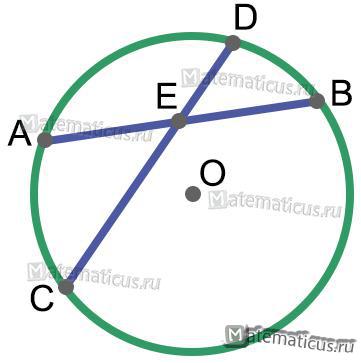
Рисунок 11
AB; CD – хорды
E — точка пересечения хорд
AE · EB = CE · ED
Если две хорды окружности пересекаются, то произведение отрезков одной хорды AB равно произведению отрезков другой хорды CD
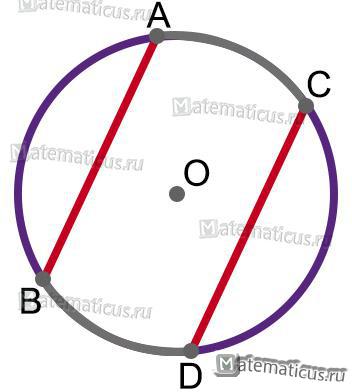
Рисунок 12
Если хорда AB равна хорде DC, то их дуги тоже равны, т.е.
AB=DC ⇒ ∪AB=∪DC
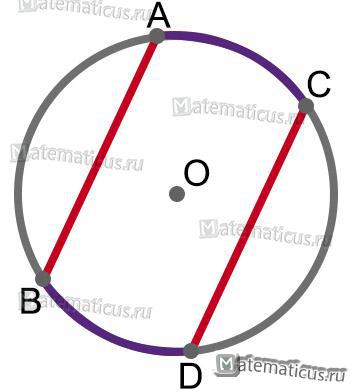
Рисунок 13
Если хорда AB параллельна хорде DC, то их дуги равны, т.е.
AB//DC ⇒ ∪AB=∪DC
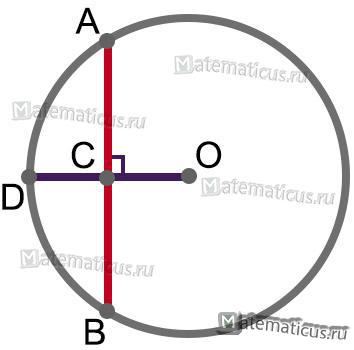
Рисунок 14
Если радиус окружности OD перпендикулярен хорде AB, то он делит хорду пополам в точке их пересечения С, т.е.
OD⊥AB ⇒ ∪AC=∪BC
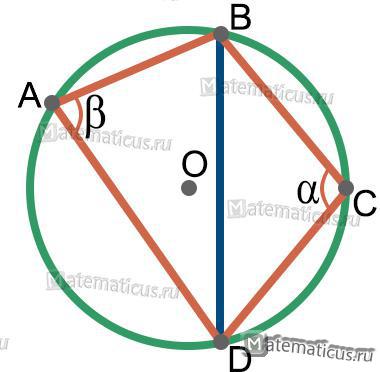
Рисунок 15
Сумма двух вписанных углов, опирающих на одну хорду и находящихся по разные стороны от нее, равна 180°, т.е.
α + β = 180°
Рисунок 16
Задача 1
Хорды AB и CD пересекаются в точке E. Найдите ED, если AE = 5, BE = 2, CE = 2,5.

Решение
По свойствам хорды имеем
АЕ·ЕВ=СЕ·ЕD
5·2=2,5·ЕD
10=2,5·ЕD
Отсюда
ED=4
Задача 2
Хорда AB стягивает дугу, равную 119°, а хорда AC – дугу, равную 43°. Найдите угол BAC.
Решение
∠ВАС равен половине дуги на которую опирается
Дуга равна 3600-1190-430=1980
Угол BAC равен:
$\angle{BAC}=\frac{198}{2}=96$
