Признаки равенства треугольников
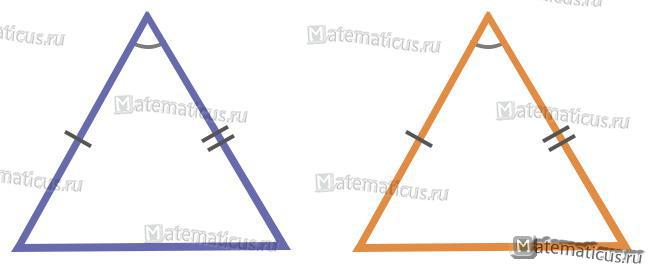
- По двум сторонам и углу между ними.
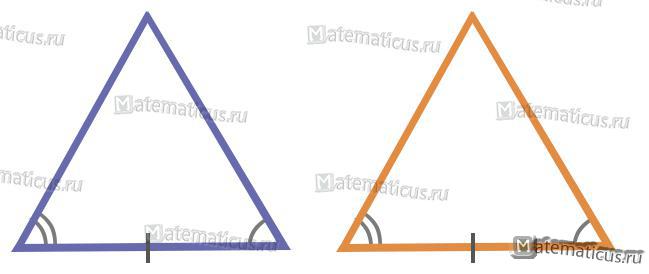
2. По одной стороне и двум прилежащим к ней углам.
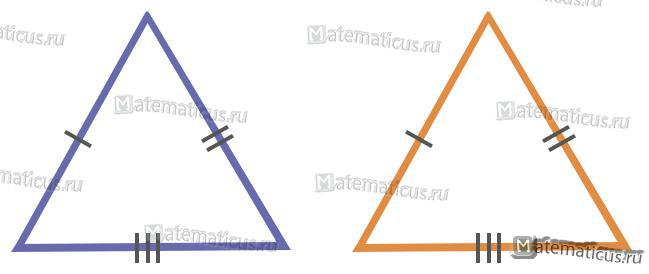
3. По трём сторонам.
Признаки подобия треугольников
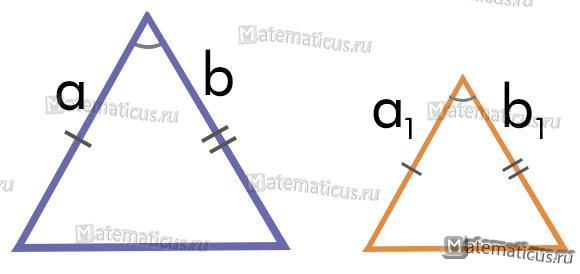
- По двум пропорциональным сторонам и углу между ними:
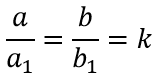
где k – коэффициент подобия
2. По двум равным углам
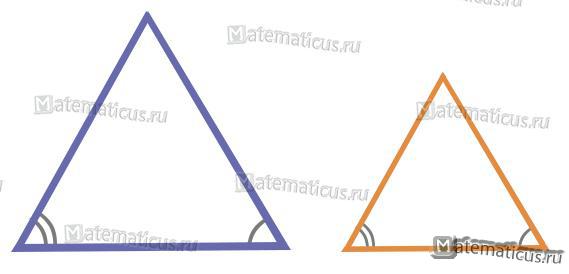
3. По трём пропорциональным сторонам
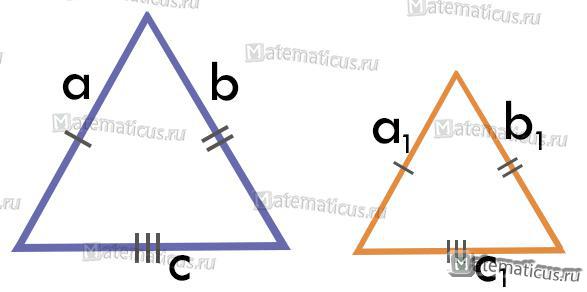
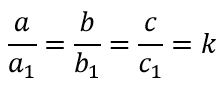
где k – коэффициент подобия
Задача о подобии треугольников
Прямая, параллельная стороне AB в треугольнике ABC, делит сторону AC в отношении 2 : 7, считая от вершины A. Найдите периметр отсеченного треугольника, если AB = 10 см, BC = 18 см, CA = 21,5 см.
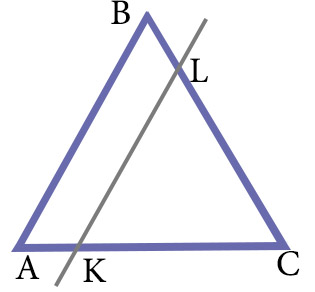
Решение
KL||АВ — по условию задачи;
∠KLC=∠В, ∠CKL=∠А — признаки подобия треугольников по двум равным углам;
∠С — общий угол.
Отсюда следует, что треугольники KLC и АВС подобны.
Коэффициент подобия равен:
$k=\frac{2+7}{7}=\frac{9}{7}$
Отношение треугольников равно:
$\frac{P_{ABC}}{P_{KLC}}=\frac{9}{7}$
Периметр треугольника АВС равен:
$P_{ABC}=10+18+21,5$
Отсюда находим периметр отсеченного треугольника KLC:
$\frac{49,5}{P_{KLC}}=\frac{9}{7}$
$P_{KLC}=\frac{49,58\cdot7}{9}=38,5$