Треугольник

Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника). По сути это самый простой многоугольник.

Виды треугольников

Рассмотрим виды треугольника, в зависимости от их свойств.

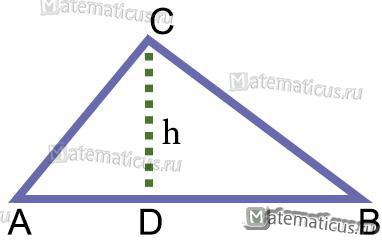
Рисунок 1

Если все углы острые, то такой треугольник — остроугольный (рис.1).

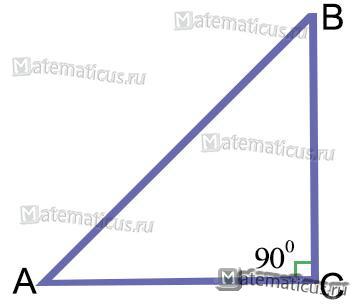
Рисунок 2

Если один из углов прямой  ∠С=90⁰, а остальные ∠A и ∠B — острые, то такой треугольник — прямоугольный (рис.2).

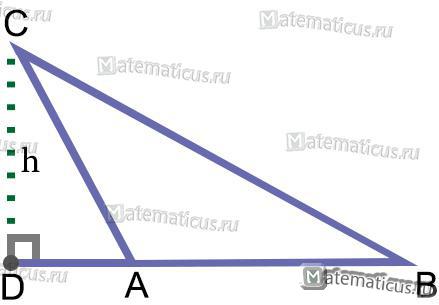
Рисунок 3

Если один из углов тупой — ∠A, а остальные ∠C и ∠B — острые, то треугольник — тупоугольный (рис.3).

Равносторонний (правильный) треугольник

Равнобедренный треугольник

---

Произвольный треугольник

Произвольный треугольник — это треугольник, у которого нет равных углов, сторон (как например у равностороннего или равнобедренного треугольника), отсутствует угол 90⁰ (как например у прямоугольного треугольника).

Свойства треугольника

1. Сумма углов треугольника равна 180°, то есть (рис. 4):

α+β+γ=180°

 

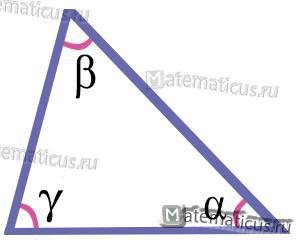
Рисунок 4

2. Внешний угол равен сумме двух внутренних не смежных с ним углов (рис. 5):

δ=α+β

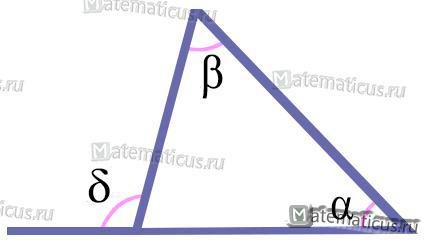
Рисунок 5

3. Неравенство треугольника заключается в том, что любая сторона треугольника меньше суммы двух других сторон, но при этом больше их разности по модулю:

|a-b| < с <a+b 

---

Свойства высот треугольника

1. Высоты треугольника пересекаются в одной точке, в точке M (рис.6). Эта точка называется ортоцентром.
2. Высоты треугольника обратно пропорциональны сторонам и формула имеет вид (рис.6):

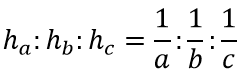
3. Формула для определения длины высоты к стороне a:

h_a=b·sinC=c·sinB

или

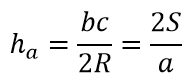
где R — радиус описанной окружности (рис.9)
S — площадь Δ

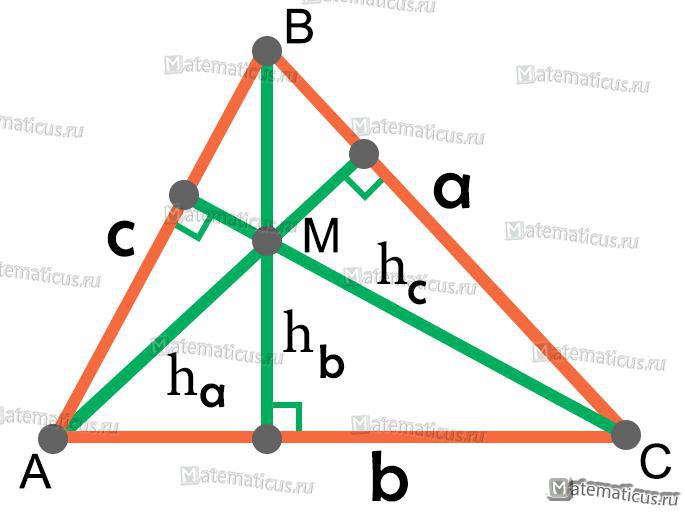
Рисунок 6

---

Средняя линия треугольника

Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.

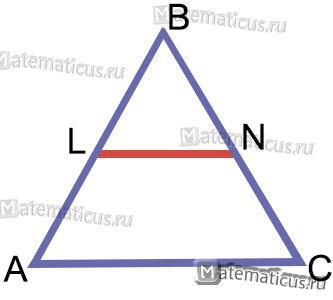
Рисунок 7

Формула для определения средней линии треугольника (рис.7):

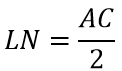
Формула периметра треугольника:

P=a+b+c

Формула полупериметра треугольника:

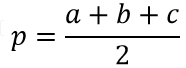
Формулы для нахождения площади произвольного треугольника

Площадь треугольника по формуле Герона:
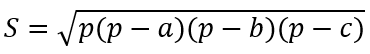, где р — полупериметр.
Формула площади произвольного треугольника через две стороны и угла между ними (рис.8):

S=b·c·sinγ

Формула площади произвольного треугольника через высоту и основания (рис.8):

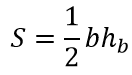
где h_b – высота опущенная на сторону b

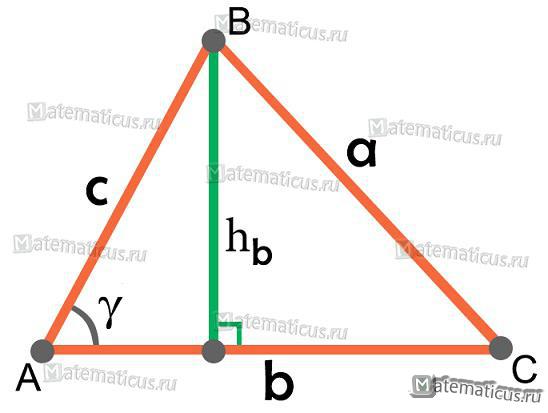
Рисунок 8

Площадь треугольника через радиусы (рис.9):

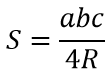
S=rp

где
R — радиус описанной окружности
r — радиус вписанной окружности
Радиус вписанной окружности в треугольник (рис.9):

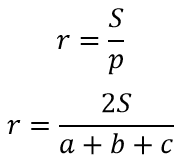
Радиус описанной окружности в треугольник (рис.9):

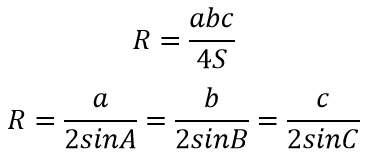
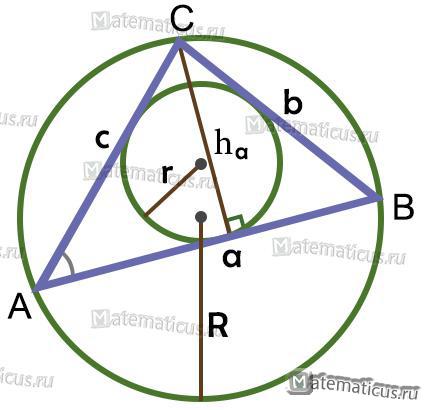
Рисунок 9

---

См. также Признаки равенства и подобия треугольников
Теорема косинусов и теорема синусов
Медиана, высота и биссектриса треугольника