Конус (от греч. «сосновая шишка») — это тело вращения, образованное вращением прямоугольного треугольника вокруг одного из своих катетов (этот катет рассматривается как ось конуса).

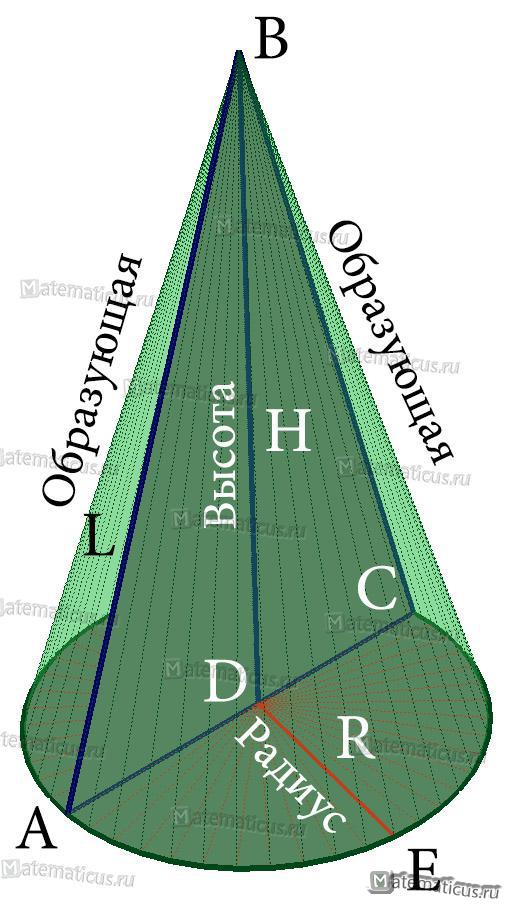
Образующая конуса —  отрезок (как пример на рисунке это отрезок AB=L), соединяющий вершину конуса с любой точкой, лежащей на границе основания.

Высота конуса — это перпендикуляр DB, опущенный из вершины конуса в центр основания.

Ось конуса  — это прямая, проходящая через центр круга и вершину конуса.

Радиус основания — это радиус конуса DE.

Вершина конуса на рисунке точка B.

Осевое сечение конуса – это сечение, содержащее ось.

Н — высота конуса;

R — радиус основания.

Формула для нахождения площади боковой поверхности конуса:

S=πRL

Площадь полной поверхности конуса равна:

S=S_бок+S_осн=πRL+ πR²

Формула для определения объёма конуса:

V=$\frac{1}{3}$πR²H

Свойства конуса

1. Все образующие конуса равны.
2. Углы наклона образующих к основанию равны.
3. Углы между осью и образующими равны.
4. Углы между осью и основанием прямые.

Усеченный конус

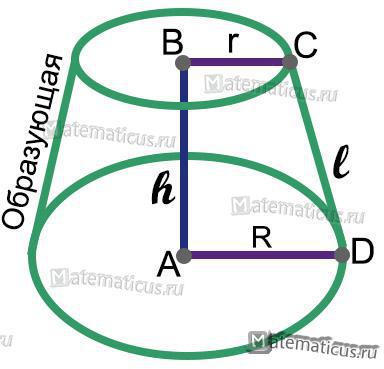
Усеченный конус — часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.

Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

R — радиус нижнего основания;

r — радиус верхнего основания;

h — высота конуса.

Формула для определения объёма усеченного конуса:

V=$\frac{1}{3}$πh(r²+rR+R²)

Формула для определения площади боковой поверхности усечённого конуса:

S=πL(r+R)

Площадь полной поверхности усечённого конуса:

S= S_бок+S_осн1+S_осн2=πL(r+R)+πR²+πr²

---

Задача
Угол между образующей и осью конуса 30°. Образующая равна 12 см. Найдите площадь полной поверхности и объем конуса.
Решение

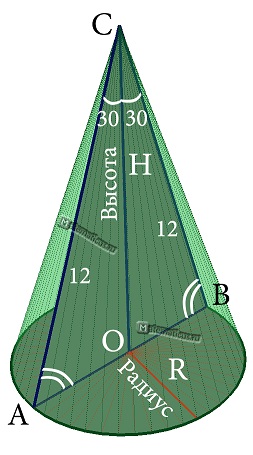
ΔCAB — правильный, так как CA=CB=AB=12 см.
$CO = \frac{{\sqrt 3 }}{2} \cdot 12 = 6\sqrt 3 $
Площадь полной поверхности конуса равна:
S_пов=πR(r+R)=π·6·(12+6)=108π
Объем конуса равен:
$$V = \frac{1}{3}\pi {R^2} = \frac{1}{3}\pi \cdot {6^2} \cdot 6\sqrt 3 = 72\sqrt 3 \pi $$