Пирамидой называют многогранник, у которого одна из граней является произвольным многоугольником (или треугольником или четырёхугольником и т.д. см. рис. 1), а остальные боковые грани — треугольники с общей вершиной.
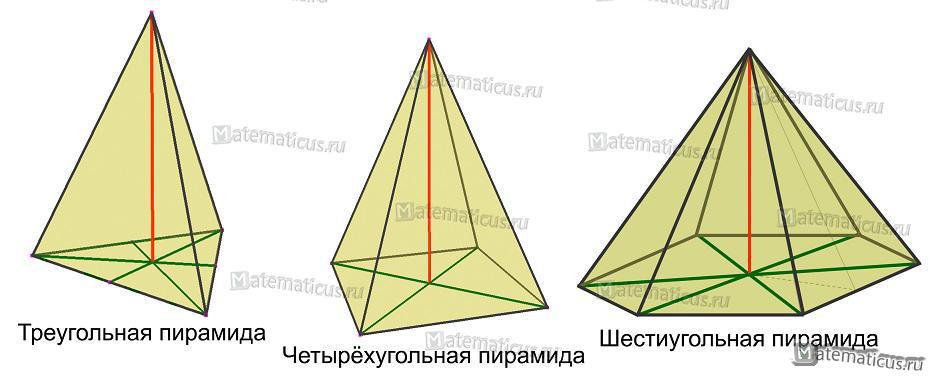
Рисунок 1
Правильная пирамида — это пирамида, в основании которой лежит правильный многоугольник и перпендикуляр, опущенный из вершины проецируется в центр этого основания.
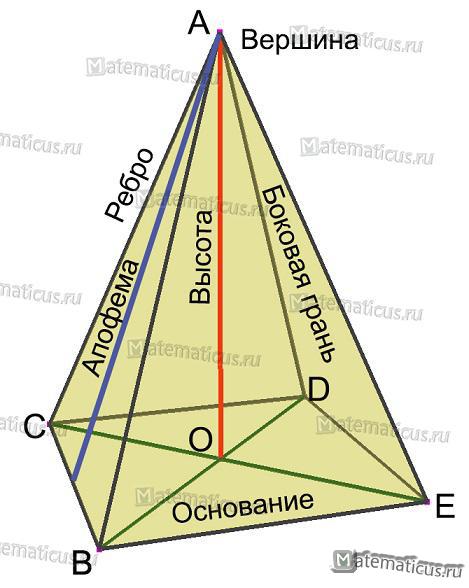
Рисунок 2
Основание пирамиды называется одна из его граней в виде произвольного многоугольника. На (рис. 2) — основанием является четырехугольник BCDE.
Боковые грани — треугольники с общей вершиной. Как пример эта грань ADE.
Боковые рёбра – это стороны боковых граней. В качестве примера ребро AC.
Вершиной пирамиды называется общая вершина боковых граней. На (рис. 2) это точка A.
Апофема — высота боковой грани правильной пирамиды. Одна из апофем пирамиды (рис. 2) — AP.
Высотой пирамиды является перпендикуляр, проведённый из вершины пирамиды в центр основания, то есть AO.
Свойства правильной пирамиды
- Все боковые ребра равны между собой.
2. Все боковые грани — равные равнобедренные треугольники.
3. Все апофемы боковых граней имеют одинаковую длину.
4. Двухгранные углы при ребрах основания равны.
5. Двухгранные углы при боковых ребрах равны.
6. Все плоские углы при вершине равны.
7. В любую правильную пирамиду можно вписать сферу.
Площадь полной поверхности пирамиды:
S=Sосн.+Sб.п.
где Sосн. — площадь основания, Sб.п. — площадь боковой поверхности.
Формула объёма пирамиды:
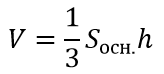
Формула боковой площади правильной пирамиды:
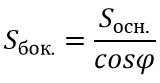
где φ — двухгранный угол при ребре основания пирамиды.
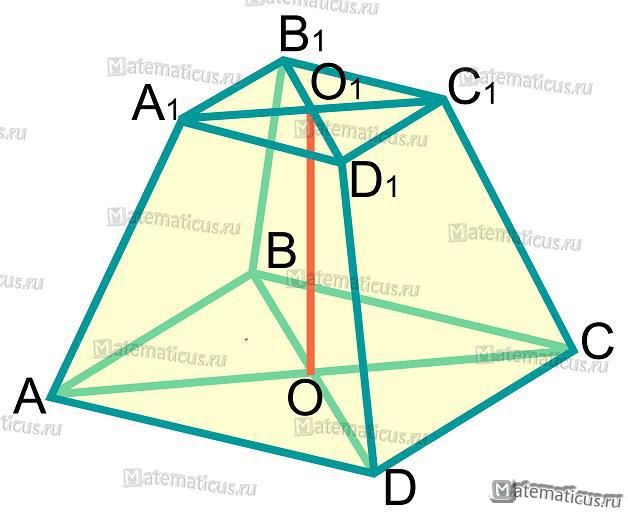
Усеченная пирамида
Усеченной пирамидой называют часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды. Боковыми гранями являются трапеции.
Формула боковой площади правильной усеченной пирамиды:
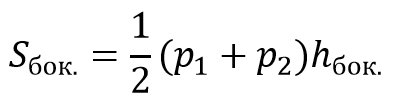
где p1 и p2 — периметры
hбок. — высота боковой грани
Формула объёма усеченной пирамиды:
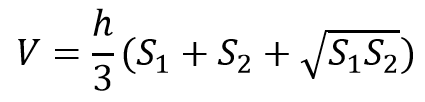
где S1 и S2 — площади оснований
h — высота
