Призма

Призма – (от греч. «присма» перев. как «опиленная» или «опиленное бревно») — многогранник, две грани — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.

Типовые виды призм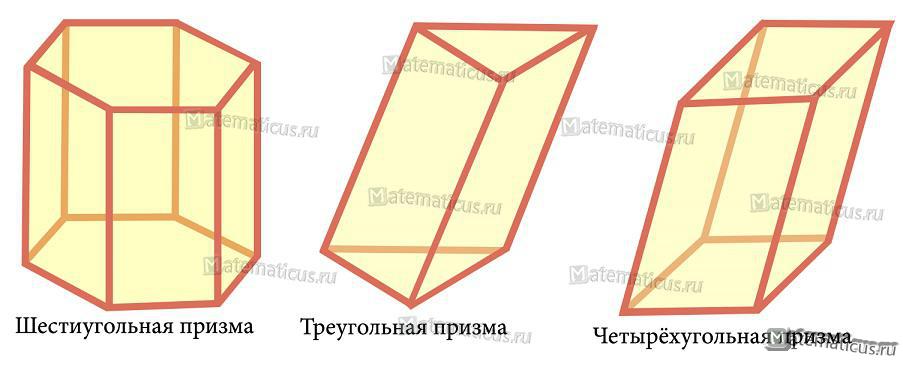

Правильной призмой называется прямая призма, основанием которой является правильный многоугольник.

Призма называется прямой, если боковые ребра перпендикулярны основаниям.

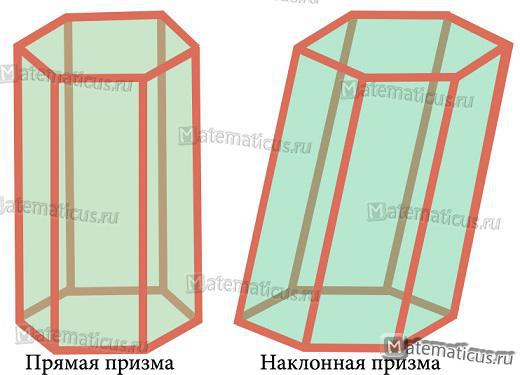
Перпендикулярное сечение – это сечение призмы плоскостью, перпендикулярной боковому ребру.

---

Свойства призмы

1. Основания призмы — равные многоугольники.
2. Боковые ребра призмы параллельны и равны.
3. Боковые грани призмы являются параллелограммами.
4. Диагонали пересекаются в одной точке и делятся в ней пополам.
5. В основании призмы может лежать любой многоугольник.
   

   ---

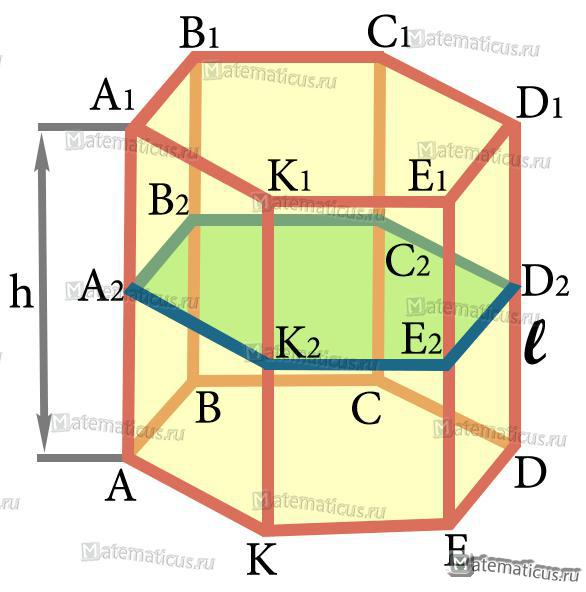
A₂B₂C₂D₂E₂K₂ — сечение
ABCDEK и A₁B₁C₁D₁E₁K₁ — основание
DD₁ — как пример, боковое ребро

Формула боковой поверхности площади призмы:

S_бок = P_сеч·L

Формула площади полной поверхности призмы:

S_полн= S_бок+2S_осн

Формула объема призмы:

V=S_осн·h=S_сеч ·L

где

S_осн. — площадь основания призмы;

h — высота призмы;

S_сеч — площадь сечения, перпендикулярного боковому ребру;

L – длина бокового ребра;

P_сеч — периметр сечения, перпендикулярного боковому ребру

Прямая призма

Формула площади боковой поверхности прямой призмы:

S_бок = P_осн·L

где

Формула площади полной поверхности прямой призмы:

S_полн= S_бок+2S_осн

Объем прямой призмы:

V=S_осн·L

где

Р_осн — периметр основания прямой призмы;
а — боковое ребро;
S_бок — площадь боковой поверхности прямой призмы;

S_осн. — площадь основания прямой призмы;

L – длина бокового ребра.