Закон сообщающихся сосудов, также известный как закон Паскаля, утверждает, что если в нескольких сосудах, соединенных трубками или каналами, находится однородная жидкость, то изменение давления в любом из этих сосудов будет равномерно распространяться по всей жидкости.
Это означает, что если в одном из сосудов изменяется давление (например, из-за добавления или удаления жидкости), то это изменение давления мгновенно распространится на все остальные части жидкости в системе.
Закон сообщающихся сосудов для однородной жидкости
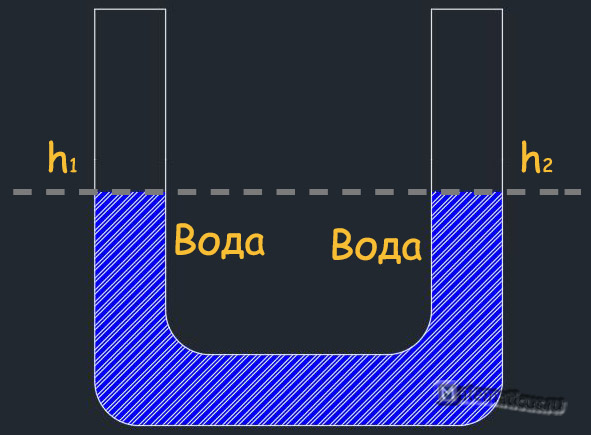
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаковое).
Гидростатическое давление, оказываемое на жидкость в каком-либо одном месте на ее границе, передается без изменения во всех точках жидкости и определяется по формуле:
p=ρgh
р — давление столба жидкости, Па;
ρ — плотность жидкости, кг/м3;
g — ускорение свободного падения, м/с2;
h — высота столба жидкости, м.
h1=h2
p1=p2
Закон сообщающихся сосудов для неоднородной жидкости
В сообщающихся сосудах, в которых содержится разные жидкости, при равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба с меньшей плотностью.
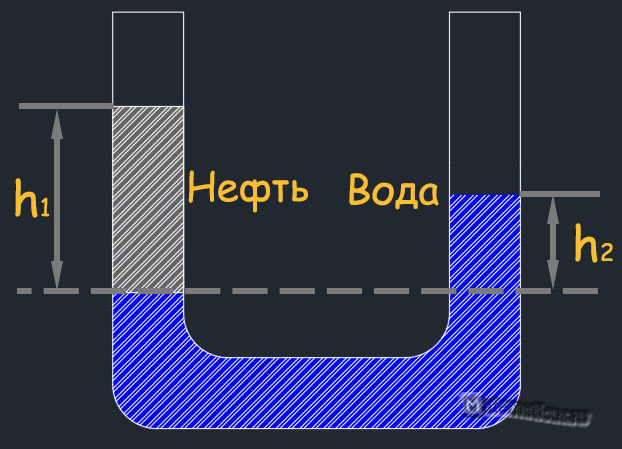
ρ1h1=ρ2h2
h1>h2
p1<p2
Закон сообщающихся сосудов открыт Паскалем.
Закон о сообщающихся сосудах применяется в морских шлюзах для движения кораблей, автомобильных баках для измерения уровня топлива, фонтанах, водонапорных башнях, лейках и т.д.
Задача
Справедлив ли закон сообщающихся сосудов в условиях невесомости? Объясните почему.
Решение
Закон сообщающихся сосудов в условиях невесомости не действует, так как жидкость в состоянии невесомости не обладает весом (вес тела равен нулю) и поэтому жидкость не оказывает давление на дно сосуда.
