Произведение всех натуральных чисел от 1 до n включительно называется n-факториалом и обозначается как n! и равен
$${\bf{n}}! = {\bf{1}} \cdot {\bf{2}} \cdot {\bf{3}}…\left( {{\bf{n}} — {\bf{1}}} \right) \cdot {\bf{n}}$$
Эту формулу можно записать в следующем виде:
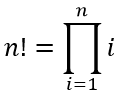
Factor от лат. сомножитель.
Примечание
Факториал определён только для целых неотрицательных чисел
Формула Муавра-Стирлинга, для приближённого вычисления факториала:
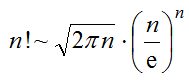
Факториал вычисляется через Гамму-функцию по формуле:
$x! = \Gamma \left( {x + 1} \right)$
$\Gamma\left( x \right) = \left( {x — 1} \right)!$
Свойство факториала:
- Основное свойство (рекурсия)
$${\bf{n}}! = \left( {{\bf{n}} — {\bf{1}}} \right)! \cdot {\bf{n}}$$
Псевдокод:
int FactorialR(int num)
{
if(num==0) return 1;
return num*FactorialR(num - 1);
}
2. Для числа 0 принято соглашение
$${\bf{0}}!{\text{ }} = {\text{ }}{\bf{1}}$$
3.
$${\bf{n}}{!^{\bf{2}}} \geqslant {{\bf{n}}^{\bf{n}}} \geqslant {\bf{n}}! \geqslant {\bf{n}}$$
Факториал часто используется в формулах комбинаторики (размещение без повторений, сочетание с повторениями и сочетание без повторений, перестановка с повторениями и перестановка без повторений), теории вероятностей (формула Бернулли) и т.д.
Пример 1
5!= 1⋅2⋅3⋅4⋅5 =120
Пример 2
9!-7!=1⋅2⋅3⋅4⋅5⋅6⋅7⋅8⋅9−1⋅2⋅3⋅4⋅5⋅6⋅7=
=1⋅2⋅3⋅4⋅5⋅6⋅7⋅(8⋅9−1)=5040⋅71= 357840
