Число различных перестановок с повторениями из элементов {а1, a2,… аn}, в которых элементы а1, a2,… аn повторяются соответственно i раз, равно: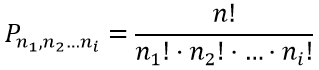
Это формула комбинаторики называется перестановка с повторениями
Пусть имеется множество, состоящее из трех букв {А, A, B}.
Тогда составим различные комбинации перестановки без повторения из трех букв по 2 одинаковых элемента и одному разному, получаем: АAВ, ABA, BAA.
Пример
Сколько слов можно составить, переставив буквы в слове «математика»?
Решение
Слова «математика» состоит из 10 букв, где некоторые буквы повторяются. Число повторений «м» — 2 раза, «а» — 3 раза, «т» — 2 раза, «e», «и», «к» — 1 раз.
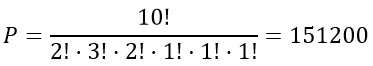

А как посчитать сколько комбинаций из 3х букв можно составить из этого слова?
Если буквы все три разные, то количество слов $p=\frac{3!}{1!1!1!}=6$
Если две буквы одинаковые, то количество слов $p=\frac{3!}{1!2!}=3$