Допустим имеется множество m, состоящее из трех букв {А, В, С}.
Составим различные комбинации размещение без повторений из двух букв n,
имеем: АВ, BС, CA, AC, BA, CB.
Эти комбинации отличаются друг от друга только расположением букв или самими буквами.
Обозначение: $A_n^m$
Формула для определения размещение без повторений:
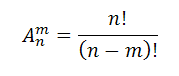
Пример
На пятом курсе изучается 7 предметов. Сколькими способами можно составить расписание занятий на один день, если в учебный день разрешается проводить занятия только по трём разным предметам?
Решение
Применим формулу комбинаторики размещение без повторений, имеем
$A_7^3 = \frac{{7!}}{{\left( {7 — 3} \right)!}} = \frac{{7!}}{{4!}} = 5\cdot6\cdot7 = 210$
6229