Сочетание без повторений

Сочетанием без повторений называют комбинации, составленные из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом.

Обозначение: $С_n^m$

Допустим, имеется три буквы А, В и С.

Составим всевозможные комбинации только из двух букв, которые отличаются друг от друга хотя бы одним элементом: АВ, АС, ВС.

При подсчете числа сочетаний элементов — порядок не важен.

Запишем формулу сочетания

---

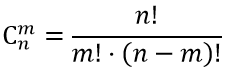
Пример 1

В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства? Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем

---

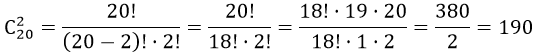
Пример 2

Пусть имеется множество, содержащие 4 буквы: {А,В,С,D}.

Записать все возможные сочетания из указанных букв по три.

Решение

По формуле сочетания имеем,

 $C_4^3 =\frac{{4!}}{{\left( {4 — 3} \right)!\cdot3!}} = \frac{{4!}}{{3!}} = \frac{{1\cdot2\cdot3\cdot4}}{{1\cdot2\cdot3}} = 4$

---

Пример 3

В ящике 15 деталей, среди которых 6 бракованных. Наугад выбирается комплект из 5 деталей. Сколькими способами можно составить такой комплект, в котором 2 детали бракованные?

Решение

$C_{6}^2$ — количество способов выбора двух бракованных деталей из шести
$C_{9}^3$ — количество способов выбора трех исправных деталей из девяти
Тогда количество комбинаций по правилу умножения будет
$C_{6}^2·C_{9}^3=\frac{{6!}}{{(6-2)!2!}}·\frac{{9!}}{{(9-3)!3!}}=15·84=1260$

---

Пример 4

Сколькими способами можно распределить три путевки в один санаторий между пятью желающими?

Решение 
Так как путевки предоставлены в один санаторий, то варианты распределения отличаются друг от друга хотя бы одним желающим. Поэтому число способов распределения равно

---

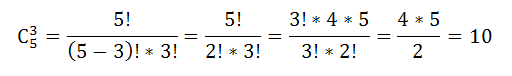
Пример 5
В научном конкурсе участвует 12 человек, из них 5 женщин и 7 мужчин. Сколькими способами можно сформировать группу из 7 человек, чтобы в ней было 3 женщины?

Решение 
Из пяти женщин необходимо выбрать по три. Следователь, число таких способов отбора равно $С_5^3$

Число способов отбора мужчин, четырех из семи равно $С_7^4$

По формуле комбинаторики – сочетания, группу можно сформировать способами:

---

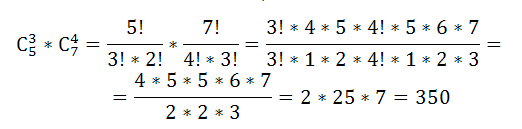
Пример 6

Сколькими способами можно составить суточный наряд по университету из одного офицера, двух сержантов и семи курсантов, если имеется 3 офицера, 6 сержантов и 30 курсантов?

Решение 
Число способов выбора офицера: $С_3^1$

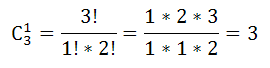
сержантов $С_6^2$

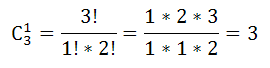
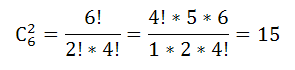
по аналогии, число комбинаций выбора курсантов, получаем $С_30^7$

 

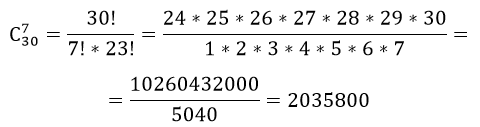
Итак, получаем число способов составления суточного наряда

$$C_3^1\cdot{C_6^2}\cdot{C_{30}^7}=3\cdot15\cdot2035800=91611000$$