Критерий Колмогорова применяется для проверки гипотезы распределения непрерывных функций СВ.
Объем выборки n≥50.
Критерий Колмогорова находится по формуле:
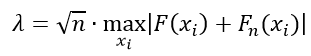
Если проведено две выборки, то формула критерия Колмогорова примет вид:
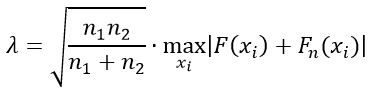
Fn(xi) — значения эмпирической функции распределения;
F(xi) — значения теоретической функции распределения.
При λ<λкр ⇒ различия между значения эмпирической функции и теоретической функции распределения не значительные ⇒ принимаем гипотезу.
Критерий Колмогорова часто применяют для проверки полученных значений в ходе эксперимента и подчиняются ли они нормальному закону распределения случайной величины.
Пример
Приведена таблица результатов исследования n=100
| Количество предметов | 1 | 2 | 3 | 4 | 5 |
| Частота | 18 | 16 | 26 | 22 | 18 |
На уровне значимости α=0,2 с помощью критерия Колмогорова определите подчиняются ли данные выборки на интервале [0,5] при n=100 равномерному закону распределения случайной величины.
Решение
Запишем функцию равномерного закона распределения случайной величины
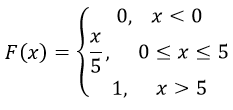
| xi | F(xi)=0,2xi | xni | Fn(xi) | |F(xi)– Fn(xi)| |
| 1 | 0,2 | 18 | 0,18 | 0,02 |
| 2 | 0,4 | 16 | 0,34 | 0,06 |
| 3 | 0,6 | 26 | 0,6 | 0 |
| 4 | 0,8 | 22 | 0,82 | 0,02 |
| 5 | 1 | 18 | 1 | 0 |
| max=0,06 | ||||
Отсюда λ=0,6 и по таблице критических значений критерий Колмогорова при α=0,2 λкр=0,65.
λ<λкр ⇒ принимаем гипотезу.

пп