Критерий Пирсона

Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:

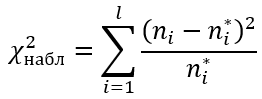
n_i – эмпирические частоты;

n_i^* – теоретические частоты;

l – количество интервалов (вариант)

Объем выборки по критерию Пирсона:

n>30

Теоретические частоты должны быть больше 5.

Распределение Пирсона с k степенями свободы рассчитывается по формуле:

k=l−r−1

r – число параметров предполагаемого распределения

Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:

k=l−3

---

Пример

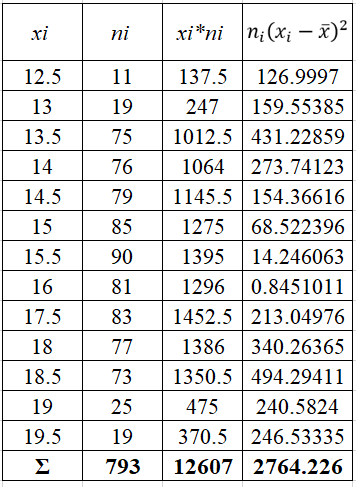
Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы

Найдем выборочное среднее по формуле: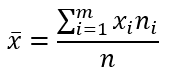

Отсюда

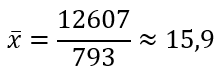
Формула выборочной исправленной дисперсии:

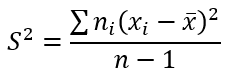
Тогда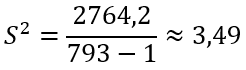

Откуда получаем выборочную исправленную СКО:

Получаем параметры нормального распределения m_x=15,9, σ=1,87.

Найдем теоретические частоты по формуле:

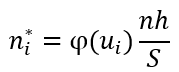
h – шаг между вариантами, h=0,5

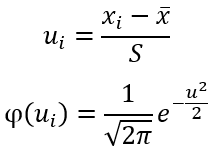
При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:

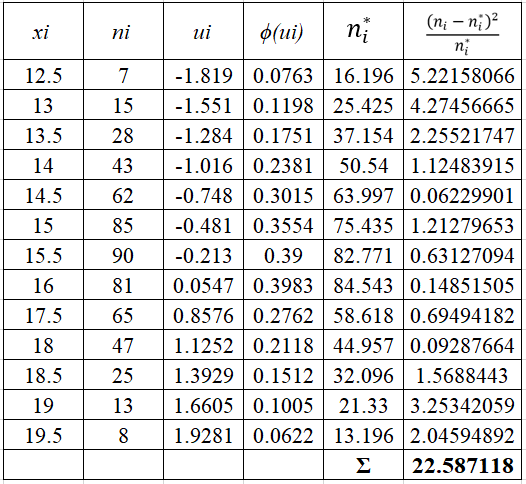
Наблюдаемое значение критерия равно:

 

Ввиду того, что

 

следовательно, нулевую гипотезу о нормальном распределении принимаем.