Критерий Стьюдента

Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины. 

 Критерий Стьюдента определяется по формуле:

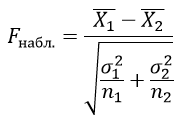
$\bar{X_1}$ – выборочные средние значения первой выборки;

$\bar{X_2}$ – выборочные средние значения второй выборки;

n₁ – объем первой выборки;

n₂ – объем второй выборки;

σ₁ и σ₂ – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:

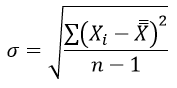
Число степеней свободы определяется по формуле:

k=n₁+n₂−2

F_кр(α, k) определяется по таблице

При F_набл<F_кр нулевая гипотеза принимается.

Формула критерия Стьюдента для несвязанных независимых выборок:

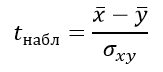
Формула для определения стандартной ошибки разности средних арифметических σ_xy:

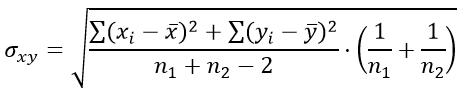
Число степеней свободы определяется выражением:

k=n₁+n₂–2

При n₁=n₂ число степеней свободы находится по формуле:

k=2n-2

а стандартная ошибка разности средних арифметических σ_xy задаётся выражением:

---

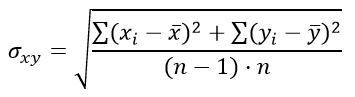
Пример

Даны две выборки.

В первой выборки продажа товара со скидкой, а во второй без скидки.

№ п/п	X	Y
1	25	19
2	34	31
3	23	17
4	35	24
5	33	28
6	25	31
7	45	39
8	41	32
9	27	38
10	54	43
11	32	21
12	32

По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?

Решение

В соответствии с таблицей n₁=12, n₂=11

Вычислим дисперсии D(X), D(Y)

№ п/п	X	Y	D(X)	D(Y)
1	25	19	78,028	107,4
2	34	31	0,0278	2,6777
3	23	17	117,36	152,86
4	35	24	1,3611	28,769
5	33	28	0,6944	1,8595
6	25	31	78,028	2,6777
7	45	39	124,69	92,86
8	41	32	51,361	6,9504
9	27	38	46,694	74,587
10	54	43	406,69	185,95
11	32	21	3,3611	69,95
12	32		3,3611
Сумма	406	323	911,67	726,55
Среднее	33,833	29,364

Подставим значения в формулу стандартной ошибки разности средних арифметических σ_xy:

 

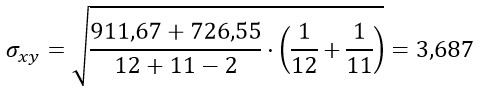
Вычисляем критерий Стьюдента:

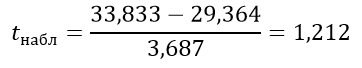
Число степеней свободы равно:

k=12+11–2=21

По таблице Стьюдента находим критическое значение:

t_крит=2,8310     

Отсюда t_крит> t_набл, следовательно, зависит.