Принцип максимума Понтрягина

Принцип максимума Понтрягина

Принцип максимума Понтрягина является ключевым результатом в оптимальном управлении и оптимальном управлении дифференциальными уравнениями. Он был разработан российским математиком Левом Понтрягиным в 1956 году.

Этот принцип предоставляет необходимые условия для оптимальности в задачах оптимального управления. Он утверждает, что если задача имеет конечное время и завершается на момент времени t, то существует функция, называемая функцией переключения, которая определяет оптимальное управление.

Принцип максимума Понтрягина формулируется в терминах функции Гамильтона-Понтрягина, которая является комбинацией функции стоимости и динамики системы. Которая утверждает, что оптимальное управление должно удовлетворять определенным условиям, связанным с этой функцией.

Условие задачи управления

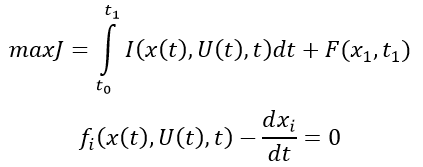
Алгоритм решения задачи оптимального управления на основе принципа максимума Понтрягина

1. Вводится n-мерный вектор сопряженный переменной Y(t), определяется функция Гамильтона

H(X,U,Y,t)=I(X,U,t)+Yf(X,U,t)

2. Составить требуемые условия существования экстремума функции max H(X,U,Y,t) при t₀≤t≤t₁

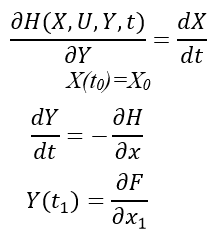
3. Найти такую функцию, которая бы удовлетворяла условию выше, то есть X(t), Y(t), U(t).