Задача коммивояжёра заключается в разовом посещение всех городов по минимальному пути (маршруту) и возвращение в искомый город.
Рассмотрим пример решения задачи коммивояжёра методом ветвей и границ
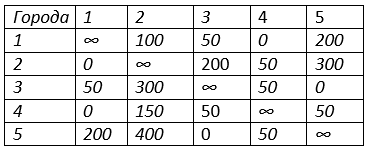
Первая итерация
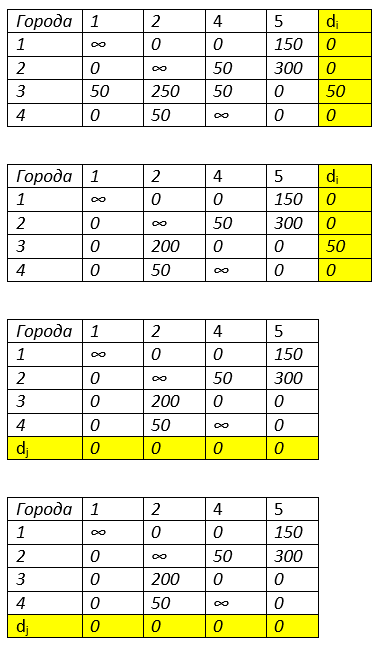
Найдём минимальные значения по строкам di
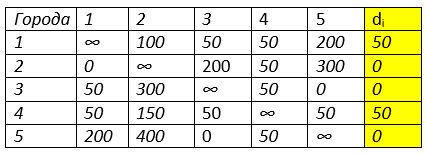
Производим редукцию по строкам путём вычитания минимального значения.
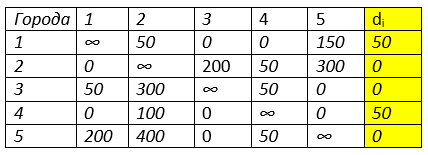
Найдём минимальные значения по столбцам dj
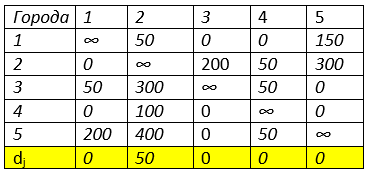
Аналогично производим редукцию по столбцам.
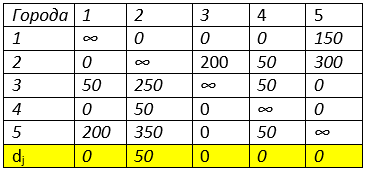
В получившейся матрице таблице находим нулевые значения
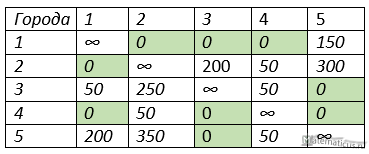
Вычисляем оценку для нулевых значений. Она заключается в отдельном поиске минимального значения по строкам относительно нулевого значения, аналогично по столбцам, затем оценка суммируется.
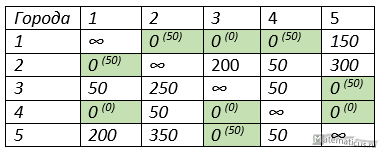
Выберем значения в таблице с максимальной оценкой
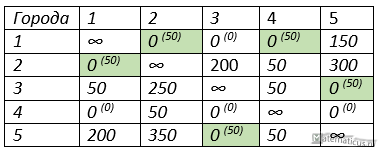
Сократим матрицу потерь за счёт исключения строки и столбца с наибольшей оценкой в нашем случае 5→3, так как это оптимальный путь, которые соответствует как городу отправления, так и городу назначения, при этом, расстоянии равно нулю.
Получаем новую матрицу потерь
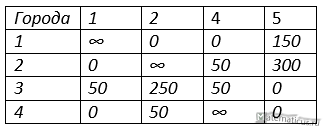
В третьей строке необходимо вместо нуля (минимального значения) поставить ∞, чтобы отсечь посещённые города.
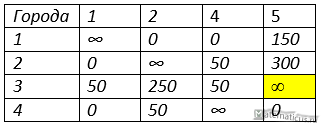
Вторая итерация решения задачи коммивояжера методом ветвей и границ, здесь всё аналогично, как и впервой итерации, проделываем те же самые операции
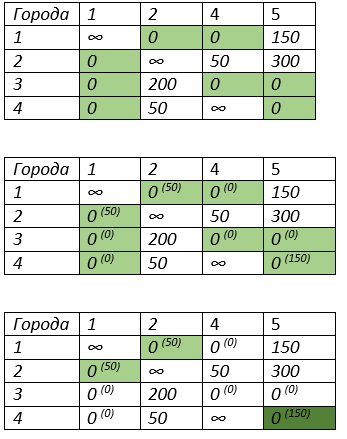
Максимальная оценка нулевого значения находится в 4 строке и 5 столбце, поэтому их сокращаем. Получаем путь 50 ед. и 4→5. Матрица потерь примет вид
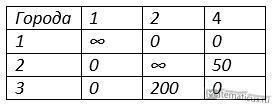
Ставим в ячейке знак ∞ на посещённые города. В нашем случае обратных путей к посещённым городам нет, поэтому в ячейке не ставим знак ∞ и матрицу оставляем без изменений.

Третья итерация решения задачи коммивояжера
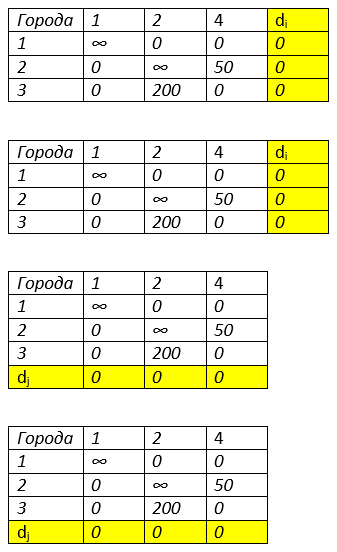
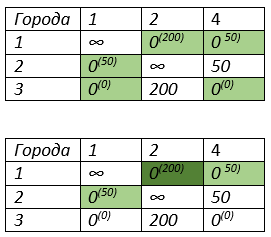
Максимальная оценка нулевого значения находится в 1 строке и 2 столбце. Получаем путь 100 ед. и 1→2.
Получим матрицу потерь 2 на 2
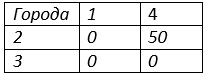
В нашем случае имеется обратный путь, поэтому ставим знак ∞ и матрица потерь будет иметь вид.
| Города | 1 | 4 |
| 2 | ∞ | 50 |
| 3 | 0 | 0 |
Четвертая итерация задачи коммивояжера методом ветвей и границ
| Города | 1 | 4 | di |
| 2 | ∞ | 50 | 50 |
| 3 | 0 | 0 | 0 |
| Города | 1 | 4 | di |
| 2 | ∞ | 0 | 50 |
| 3 | 0 | 0 | 0 |
| Города | 1 | 4 |
| 2 | ∞ | 0 |
| 3 | 0 | 0 |
| dj | 0 | 0 |
| Города | 1 | 4 |
| 2 | ∞ | 0 |
| 3 | 0 | 0 |
| dj | 0 | 0 |
| Города | 1 | 4 |
| 2 | ∞ | 0(∞) |
| 3 | 0(∞) | 0(0) |
| Города | 1 | 4 |
| 2 | ∞ | 0(∞) |
| 3 | 0(∞) | 0(0) |
Сокращаем с максимальной оценкой нулевого значения — это строка 3 и столбец 1 и получаем примитивную матрицу, в которой отсутствует обратный путь. В нашем случае оптимальный путь равен 50 ед. и 3→1.
| Города | 4 |
| 2 | 0 |
Эта матрица говорит о том, что город 2 и город 4 не замкнуты, длина пути равна 50 ед.
Таким образом, мы решили сложную задачу коммивояжёра методом ветвей и границ и нашли кратчайший путь, который равен
1→2→4→5→3→1
и длина его равна 250.
См. также
