Решение задачи линейного программирование симплекс методом искусственного базиса (М-метод)
Рассмотрим метод искусственного базиса на примере
Дана целевая функция
Z=3x1+2x2+x3→max
Ограничения в виде системы линейных уравнений
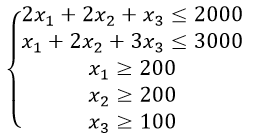
x1,x2,x3 ≥0
Для коэффициентов базисных переменных надо учитывать, что знак неравенства «≤» эквивалентен «+», а знак неравенства «≤» — «–»
В целях построения начального опорного плана ведём дополнительные переменные и приведем уравнение к каноническому виду
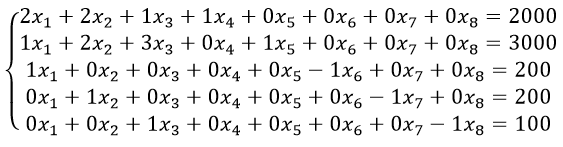
Далее, в полученную линейную систему введем также искусственные переменные
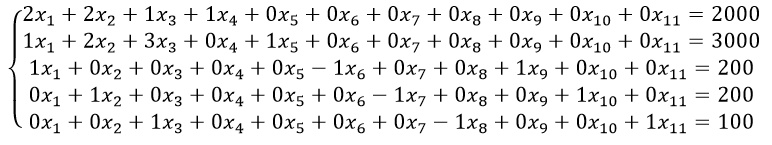
Также целевая функция при максимизации примет вид
F(x)=3x1+2x2+x3-Mx9-Mx10-Mx11
Под символом M, будем понимать очень большое неотрицательное число.
Так как необходимо максимизировать max функцию, то знак перед M ставится «-», то есть коэффициент равен -M.
Далее, из системы линейных уравнений из уравнений 3,4,5 выразим искусственные переменные x9,x10,x11, они равны
x9=200-x1+x6
x10=200-x2+x7
x11=100-x3+x8
Подставим полученные значения в целевую функцию
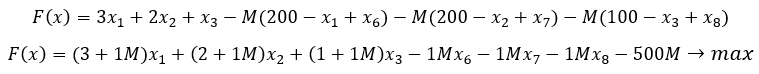
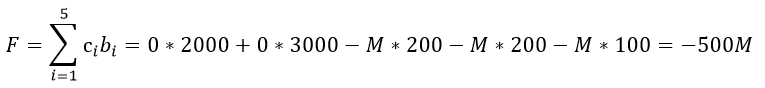
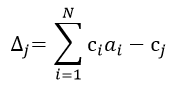
Составим 1-ый опорный план
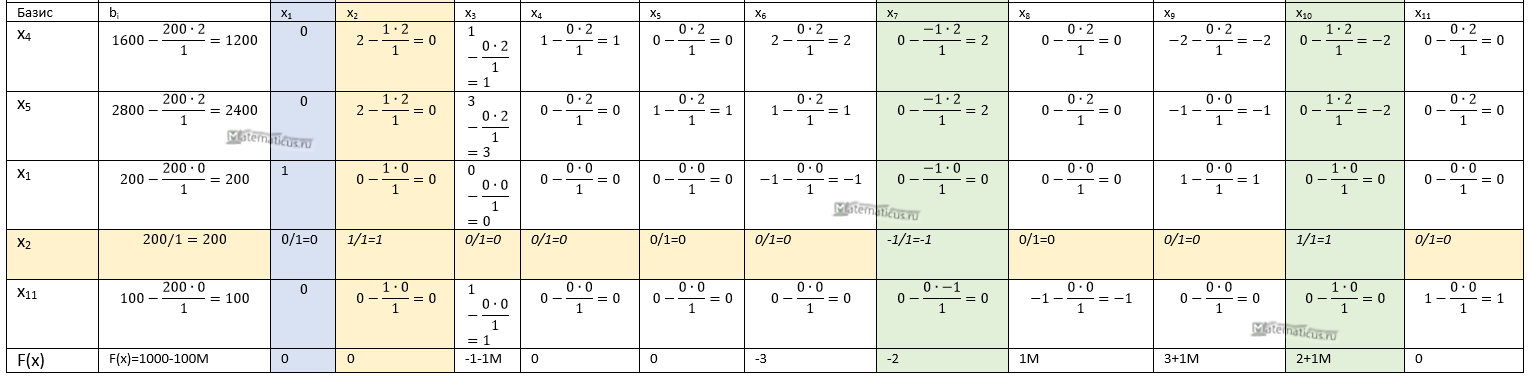
Первая итерация
Данный опорный план не оптимален в связи с тем, что в индексной строке имеются отрицательные значения.
По модулю из индексной строки выбираем наибольшее значение, и оно равно -3-1М.
По строкам найдем минимальное значение по формуле
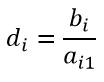
2000/2=1000
3000/1=3000
200/1=200
min{1000,3000,200,-,-}=200
Вторая итерация
Имеем на второй итерации следующий опорный план
Вторая итерация
Полученный опорный план не оптимален имеются отрицательные значения в индексной строке.
Выбираем по модулю наибольшее значение -2-1М
1600/2=800
2800/2=1400
200/1=200
min{1600,1400,-,200,-}=200
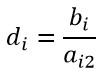
Решаем аналогично
Третья итерация
min{1200,800,-,-,100}=100
Четвертая (заключительная) итерация
План не оптимален, в индексной строке имеются отрицательные значения
min{550,2100,-,-,-}=650
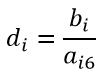
X1=750
X2=200
X3=100
F(x)=3*750+2*200+100=2750