Транспортная задача Метод потенциалов Пример решения

Метод потенциалов (оптимизация транспортных задач)

Метод потенциалов для решения транспортной задачи с наименьшей стоимостью

c_ij-(u_i+v_j)=0 при любых x_ij>0

c_ij-(u_i+v_j)>0 при любых x_ij=0

В случае

c_ij-(u_i+v_j)<0 при любых x_ij=0 произвести перестановку

Целевая функция прямой задачи имеет вид:

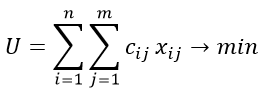
при этом

---

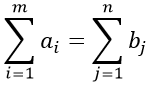
Пример решения транспортной задачи методом потенциалов
Пусть имеется опорный план, где
A — пункты отправления;
B — пункты назначения.

Ai/Bj		B1	B2	B3
		110	330	160
A1	200	3	5	2
A2	280	8	8	12
A3	120	4	6	10

Находим ячейку с самой низкой стоимостью (в соответствии с методом минимальной стоимости), в данном случае 2 и отправляем весь товар на этот склад.

Ai/Bj		B1	B2	B3
		110	330	0
A1	40	3	5	2160
A2	280	8	8	12
A3	120	4	6	10

Затем опять находим ячейку с самой минимальной стоимостью и далее проделываем аналогичные шаги.

Ai/Bj		B1	B2	B3
		70	330	0
A1	0	340	5	2160
A2	280	8	8	12
A3	120	4	6	10

Ai/Bj		B1	B2	B3
		0	330	0
A1	0	340	5	2160
A2	280	8	8	12
A3	50	470	6	10

Ai/Bj		B1	B2	B3
		0	0	0
A1	0	340	5	2160
A2	0	8	8280	12
A3	0	470	650	10

∑a=200+280+120=600
∑b=110+330+160=600
Так как a=b ресурсы совпадают с потребностями ⇒ транспортная задача закрытая.
Здесь, число известных — m+n, число уравнений — m+n-1
m+n-1=3+3-1=5 – совпадает ⇒ опорный план невырожденный.

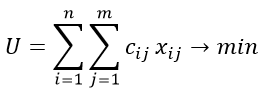
F(x)=3*40+2*140+8*280+4*70+6*50=3220

F(x)=3220

Проверка оптимальности плана

Найдём потенциалы α и β для определения оптимальности плана.

α_i+β_j=c_ij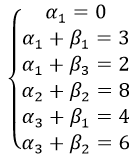

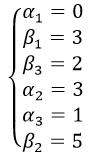
Подсчитаем оценки свободных клеток по формулам

∆_ij=с_ij-(α_i+β_j)

∆₁₂=5-(0+3)=2

∆₂₁=8-(3+3)=2

∆₂₃=12-(3+2)=8

∆₃₃=10-(1+2)=7

Так как все искомые оценки стоимости перевозки ресурсов больше нуля, то отсюда следует, что полученный опорный план оптимален.

Если мы бы получили отрицательные значения потенциалов, то опорный план был бы не оптимальным ⇒ данный план необходимо перестроить.

Для этого, из полученных отрицательных значений опорного плана выбирается то значение, которое по модулю самое наибольшее или наименьшее без модуля и ставим в соответствующей ячейки знак «+».

Затем выставляем чередующиеся знаки «–» и «+» в соответствии со следующими правилами:

— оставшиеся знаки ставим только в тех ячейках таблицы, в которых находятся значения;

— в случае, если в столбце имеется знак «–»(«+»), то в этом же столбце должен быть противоположный знак, аналогично и со строками, в случае, если в строке имеется знак «–»(«+»), то в этой же строке должен быть противоположный знак;

— цикл должен быть замкнутым.

Переходим к тем ячейкам таблицы опорного плана,  в которых содержатся знак «–» и среди них находим минимальное значение. Затем к значениям в ячейках со знаком «+» прибавляем, а в ячейках со знаком «–» вычитаем, ранее найденное минимальное значение со знаком «–», при этом ячейка с минимальным значением окажется пустой. Общее количество значений ячеек в таблице при выполнении перерасчёта должно оставаться таким же и соответствовать первоначальному условию задачи.