Показательная функция и ее свойства

Если функция, задаётся формулой вида:

 у = а^х

то такая функция называется показатель­ной.

а — положительное число a>0 и a≠1.

---

При а>1 функция у = а^х обладает следующими свойствами:

1. Область определения — D(f)=(-∞; +∞).
2.  Область значения — E(f)=(0; +∞).
3. Функция ни чётная, ни нечётная.
4.  Функция возрастает на всей числовой оси.
5. При x→∞ ось OX является горизонтальной асимптотой.
6. Экстремумов нет.

График показательной функции при а>1

---

При 0<а<1 функция у = а^х обладает следующими свойствами:

1. Область определения — D(f)=(-∞; +∞).
2.  Область значения — E(f)=(0; +∞).
3. Функция ни чётная, ни нечётная.
4.  Функция убывает на всей числовой оси.
5. При x→∞ ось OX является горизонтальной асимптотой.
6. Экстремумов нет.

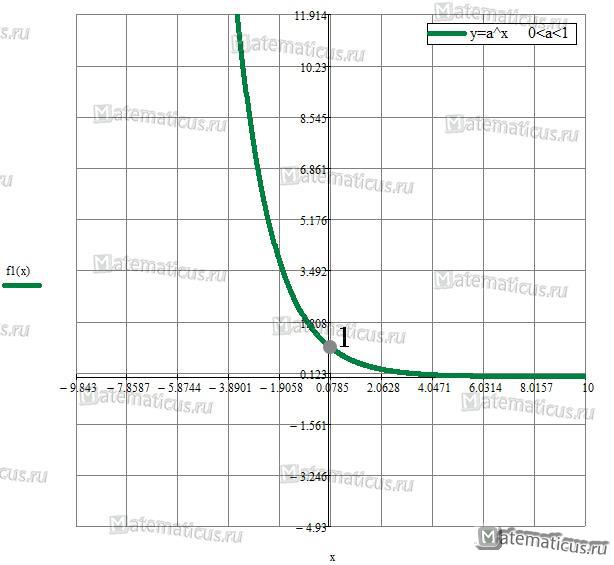
График показательной функции при 0<а<1