Функция вида:
у = хn
называется степенной функцией с натуральным показателем.
График степенной функции онлайн можете построить в этом сервисе, например, чтобы построить график функции у=х3 введите так: Math.pow(x,3)
При n=1 получаем функцию вида у = х
Рассмотрим свойства функции у = kx:
- Область определения — D(f)=(-∞; +∞).
- Область значения — E(f)=(0; +∞).
- Нечетная, так как f( — kх) = k ( — х)= — kx = -f(x)
- При k > 0 функция возрастает, а при k < 0 функция убывает на всей числовой прямой.
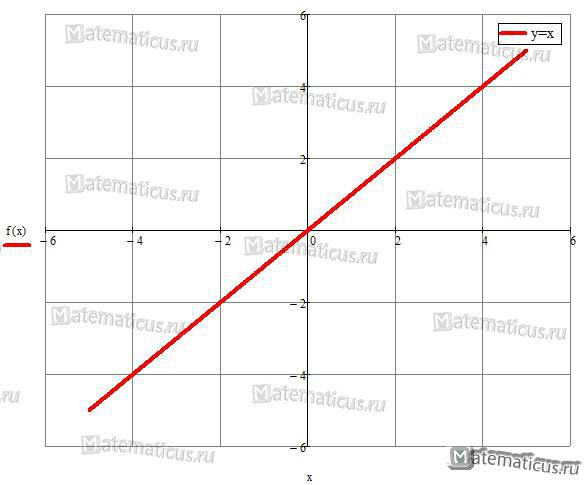
График линейной функции y=x
При n=2 получаем функцию вида у = х2 — эта функция называется параболой.
Рассмотрим свойства функции у =х2 :
- Область определения — D(f)=(-∞; +∞).
- Область значения E(f) y∈[0; +∞).
- Чётная, так как f( — х) = ( — x)2 = x2 = f (х)
- На промежутке (—∞; 0] функция убывает, а на промежутке [0; +∞) функция возрастает.
- Корень x=0
- Экстремумы функции — min при x=0.
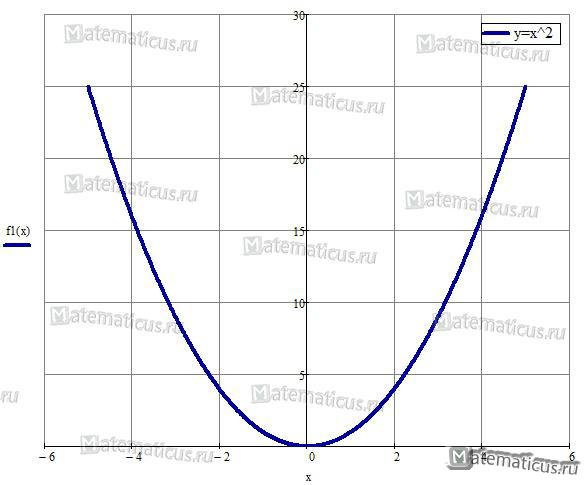
График параболы y=x2
При n=3 получаем функцию вида у = х3 — эта функция называется кубической параболой.
Рассмотрим свойства функции у = х3:
- Область определения — D(f)=(-∞; +∞).
- Область значения — E(f)=(-∞; +∞).
- Нечётная, так как f( — х) = ( — x)3 = —x3 = —f (х)
- Функция возрастает на всей числовой прямой.
- Корень x=0
- Экстремумов нет.
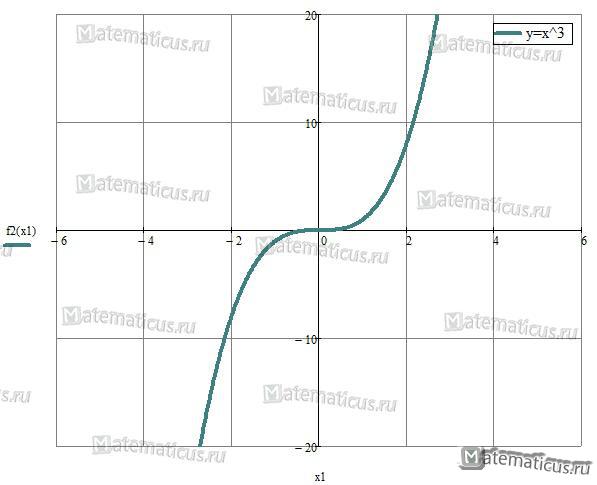
График кубической параболы y=x3
Замечание
Если n>2 и произвольное четное натуральное число (n=4, 6, 8,… .), то степенная функция обладает теми же свойствами, что и функция у=х2 и график функции напоминает параболу.
Если n>3 и произвольное нечетное натуральное число (n=5, 7, 9,… .), то степенная функция обладает теми же свойствами, что и функция у=х3 и график функции напоминает кубическую параболу.
Степенная функция с целым отрицательным показателем.
Степенная функция вида:
$$y = \frac{k}{x^n}$$
или
у = kх—n
называется степенной функцией с целым отрицательным показателем.
Рассмотрим функции при n=1 и n=2.
При n=1 получаем функцию вида $y = \frac{k}{x}$ — эта функция называется гиперболой.
Рассмотрим свойства функции $y = \frac{k}{x}$:
- Область определения — D(f)=(-∞; 0)∪(0; +∞).
- Область значения — E(f)=(-∞; 0)∪(0; +∞).
- Нечётная, так как f( — х) = k/( — x) = —k/x = —f (х)
- При k > 0 на промежутке (-∞; 0)∪(0; +∞) функция убывает, а при k < 0 на промежутке (-∞; 0)∪(0; +∞) функция возрастает.
- Экстремумов нет.
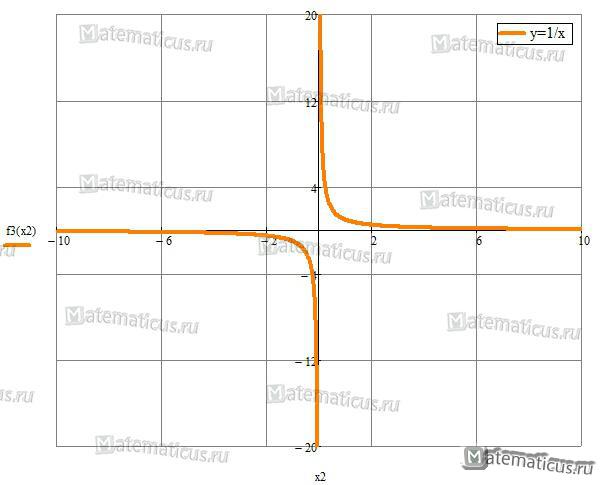
График гиперболы $y = \frac{1}{x}$
При n=2 и k=1 получаем функцию вида $y = \frac{1}{{{x^2}}}$ .
Рассмотрим свойства функции $y = \frac{1}{{{x^2}}}$:
- Область определения — D(f)=(-∞; 0)∪(0; +∞).
- Область значения — E(f)=(0; +∞).
- Чётная.
- Функция убывает на промежутке (0; +∞) и возрастает на промежутке (-∞; 0).
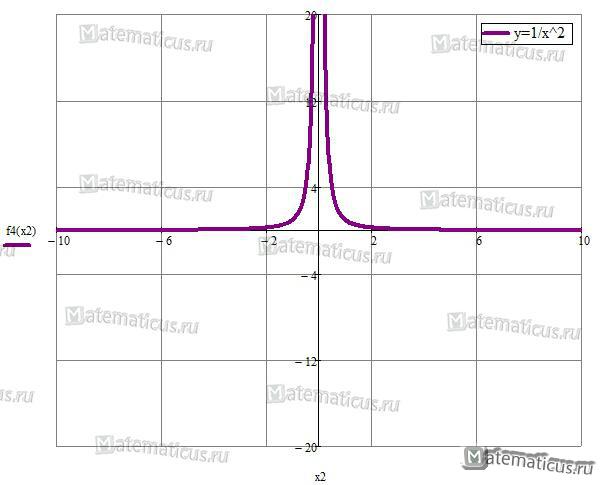
График функции $y = \frac{1}{{{x^2}}}$
Рассмотрим элементарную функцию с корнем $y = \sqrt x $
Свойства функции $y = \sqrt x $:
- Область определения — D(f)=[0; +∞).
- Область значения — E(f)=[0; +∞).
- Функция ни чётная, ни нечётная.
- Функция возрастает на [0; +∞).
- Экстремумов нет.
- Корень x=0
- Экстремумы функции — min при x=0.
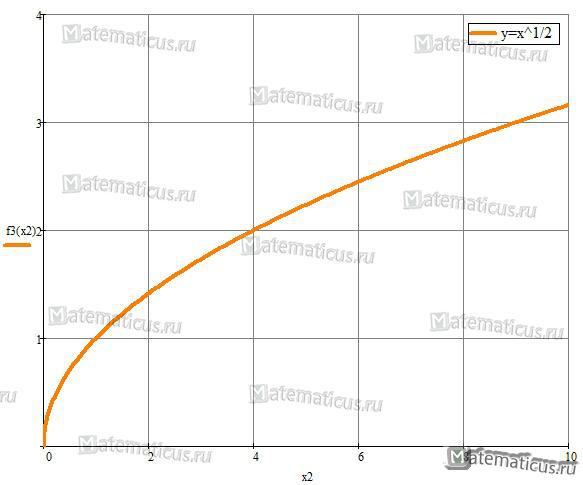

мало чего понятно