Дробь представляет число вида
![]()
где m и n целые числа и n≠0.
m — числитель;
n — знаменатель.
Замечание
Дробь 3/5 читается как три пятых.
Если числитель меньше знаменателя m<n, то дробь меньше единицы и называется правильной дробью.
Дробь 3/5— правильная дробь.
Если числитель равен знаменателю m<n, то дробь равна. Например 7/7 = 1
Если числитель больше знаменателя m<n, то дробь больше единицы и такая дробь называется неправильной.
Как пример, 27/7 — неправильные дроби.
Сокращение дроби
Если числитель и знаменатель одновременно разделить на одно и то же число, отличного от нуля, то такое действие называется сокращением дроби.
Пример

Сложение дробей
Сложение дробей с одинаковыми знаменателями выполняется по правилу:
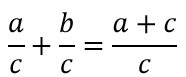
Для того, чтобы сложить дроби с разными знаменателями, нужно привести их к общему знаменателю, т.е. запишем математическое выражение
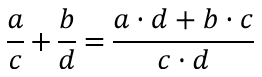
Пример
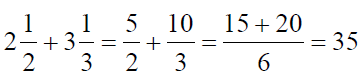
Вычитание дробей
Вычитание дробей с одинаковыми знаменателями выполняется по правилу:
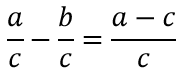
Пример
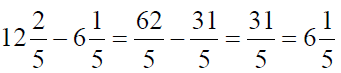
Вычитание дробей с разными знаменателями выполняется по правилу:
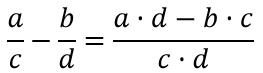
Пример
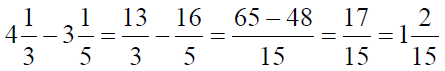
Деление дробей
Для того, чтобы разделить дробь на дробь, необходимо делимое умножить на дробь, обратную делителю.
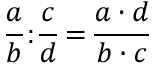
Примеры
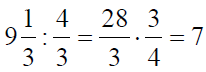
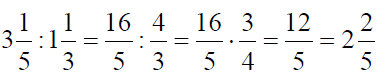
Умножение дробей
Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель умножить на знаменатель.
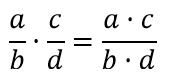
Пример
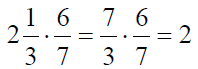
Сравнение дробей
Из двух дробей с одинаковым числителем та дробь больше, у которой знаменатель меньше.
Пример
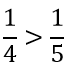
Из двух дробей с одинаковым знаменателями та дробь больше, у которой числитель больше.
Пример
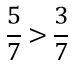
Наибольший общий делитель (НОД)
Общим делителем для нескольких натуральных чисел называется наибольшее натуральное число, служащее делителем для каждого из них.
Пример
НОД(12; 16) = 4
НОК(12; 36) = 12
12: 1, 2, 3, 4, 6,12
36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Наименьшее общее кратное (НОК)
Наименьшим общем кратным (НОК) двух чисел a и b называется наименьшее целое число, которое делится нацело как на a, так и на b.
Пример
НОК(12; 16) = 2·2·3·2·2 = 48
12 = 2·2·3
16 = 2·2·2·2
НОК(2; 3) = 6
