Перечислим основные операции над множествами с помощью диаграммы Эйлера-Венна:

---

Объединение, дизъюнкция (сумма)

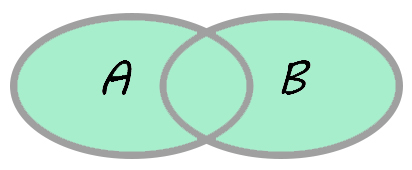
A∪B    

---

Пересечение, конъюнкция (произведение)

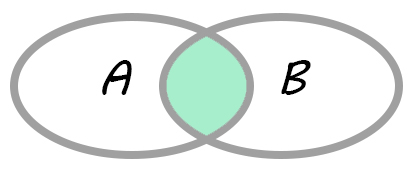
A∩B

---

Разность

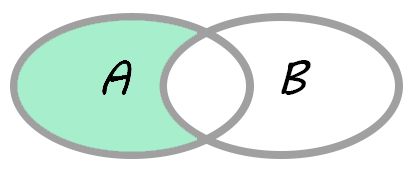
A\B

---

Симметрическая разность

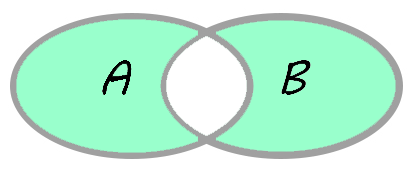
AΔB

---

Пустое множество

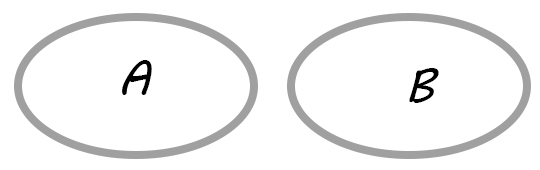
A=∅ и B=∅ – не пересекаются.

---

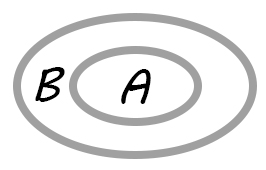
А⊂В

---

Отрицание (дополнение)

---

Основные законы теории множеств:

Коммутативность:
А ∪ В = В ∪ А

А ∩ В = В ∩ А

Ассоциативность:
А ∪ (В ∪ С) = (А ∪ В) ∪ С

А ∩ (В ∩ С) = (А ∩ В) ∩ С

Дистрибутивность:

А ∩ (В ∪ С) = (А ∩ В) ∪ (А ∩ С)
А ∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С)

Законы идемпотентности:

А ∪ A =  А

А ∩ A = А

Закон де Моргана:

$\overline {A \cup B}  = \overline A  \cap \overline B $

$\overline {A \cap B} = \overline A \cup \overline B $

Законы поглощения:
А ∪ (А ∩ В) = А

А ∩ (А ∪ В) = А

Законы склеивания:

$\left( {A \cup B} \right) \cap \left( {A \cup \overline B } \right) = A$

$\left( {A \cap B} \right) \cup \left( {A \cap \overline B } \right) = A$

Свойство единицы:

А ∪ U = U

А ∩ U = A

Закон двойного отрицания — инволюция:

$\overline{\overline A}  = A$

Закон противоречия:

$A \cap \overline A  = \emptyset $

Закон исключенного третьего (cвойство дополнения):

$A \cup \overline A  = U$

$A \cap \overline A  = \emptyset $

Операции с пустым множеством:

А ∪ ∅ = А

А ∩ ∅ = А

Преобразование разности:

$A\backslash B = A \cap \overline B $

Операции разности множеств:

А\(B\C) = (A\B)∪(A ∩ C)

(А\B)\C = (A\C)∪(B\C)

А\(B∪C) = (A\B)∩(A\C)

А\(B∩C) = (A\B)∪( A\C)