Великая теорема Ферма

Великая теорема Ферма сформулирована Пьером Фермой в 1637 году. Доказана была Эндрю Уальсом только в 1994 году на 130 страницах.

Формулировка теоремы Фермы

Для любого натурального числа n>2 уравнение

aⁿ+bⁿ≠cⁿ

не имеет решений в целых числах a,b,c (a≠0,b≠0,c≠0)

Для уравнение во второй степени:

a²+b²=c²

решением является

a=m²-n²

b=2mn

c=m²+n²

Напрмиер, пифагоровская тройка — 3, 4, 5.

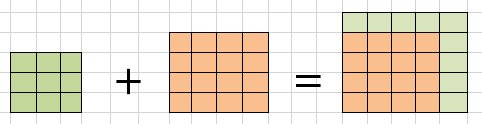
Графически это можно представить следующем образом

Для третий степени доказал в 1770 году Эйлер:

a³+b³≠c³

Для четвёртой степени доказал Ферма:

a⁴+b⁴≠c⁴

Для пятой степени доказал в 1825 году Дирихле и Лежандр:

a⁵+b⁵≠c⁵

Для седьмой степени доказал в 1839 году Ламе:

a⁷+b⁷≠c⁷

Для n<100 (за исключением степеней 37, 59, 67) доказал в 1844 году Куммер:

Полностью доказал данную теорем Эндрю Уальс.

---

Рассмотрим пример решения уравнения в n=3 степени в графическом виде:

В данном примере ближайшем решением является уравнение

6³+8³=9³-1

с отсутствием лишь одного куба. Если будем решать далее, например методом подбора, будет не хватать нескольких кубов или наоборот будет их избыток. Уравнение

a³+b³≠c³

,по сути, не разрешимо.