Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой 

Критерий среднего выигрыша

Формула критерия среднего выигрыша

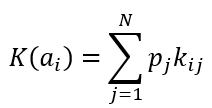
Формула оптимального решения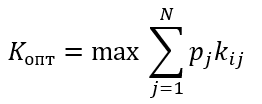

Пример

Пусть даны вероятности, p₁=0.2 p₂=0.1 p₃=0.3 p₄=0.2, тогда получаем

K(a₁)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a₂)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a₃)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a₄)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
K_опт=max{0.27; 0.48; 0.43; 0.51}=0.51

В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.

Критерий Вальда или пессимизма

Формула критерия Вальда или максимина

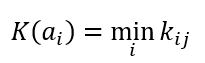
Формула оптимального решения по критерию Лапласа

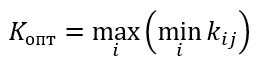
Пример

K(a₁)=min(0.4;0.5;0.3;0.4)=0.3
K(a₂)=min(0.3;0.2;0.3;0.5)=0.2
K(a₃)=min(0.6;0.3;0.3;0.2)=0.2
K(a₄)=min(0.4;0.5;0.2;0.3)=0.2
K_опт=max{0.3; 0.2; 0.2; 0.2}=0.3

По критерию Вальда оптимальным решением является выбор первой программы.

Критерий максимакса или оптимизма

Формула критерия максимакса

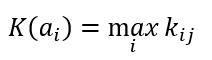
Формула оптимального решения по критерию максимакса

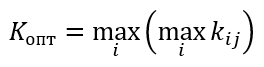
Пример

K(a₁)=max(0.4;0.5;0.3;0.4)=0.5
K(a₂)= max (0.3;0.2;0.3;0.5)=0.5
K(a₃)= max (0.6;0.3;0.3;0.2)=0.6
K(a₄)= max (0.4;0.5;0.2;0.3)=0.5
K_опт=max{0.5; 0.5; 0.6; 0.5}=0.6

По критерию максимакса оптимальным решением является выбор третьей программы.

Критерий Лапласа

Формула критерия Лапласа

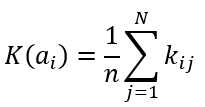
Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a₁)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a₂)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a₃)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a₄)=0.25*(0.4+0.5+0.2+0.3)=0.35
K_опт=max{0.4; 0.325; 0.35; 0.35}=0.4

По критерию Лапласа оптимальным решением является выбор первой программы.

Критерий Гурвица

Пример

Формула критерия Гурвица

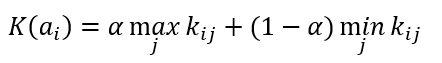
Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.

Пусть α=0.7

K(a₁)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a₂)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a₃)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a₄)= 0.7* 0.5+(1-0.7)*0.2=0.41
K_опт=max{0.44; 0.41; 0.48; 0.41}=0.48

По критерию Гурвица оптимальным решением является выбор третьей программы.

Критерий Сэвиджа или минимакса (критерий потерь)

Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа

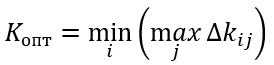
Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a₁)= max{0.2; 0; 0; 0.1}=0.2
K(a₂)= max{0.3; 0.3; 0; 0}=0.3
K(a₃)= max{0; 0.2; 0; 0.3}=0.3
K(a₄)= max{0.2; 0; 0.1; 0.2}=0.2
K_опт=min{0.2; 0.3; 0.3; 0.2}=0.2

По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.

Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.