Формула Пуассона примеры

Формула Пуассона имеет вид:

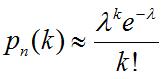
, где  λ=n·p
При большом количестве испытаний n≥100 и малых значений вероятности р≤0.1, вместо формулы Бернулли применяют формулу Пуассона (закон редких событий).
Рассмотрим применение формулы Пуассона в решение задач.

Вывод формулы Пуассона через формулу Бернулли

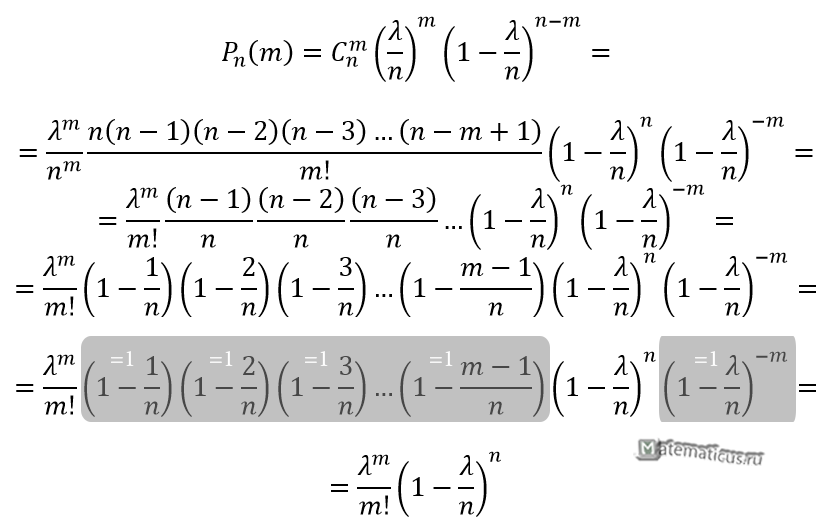
Отсюда через предел n→∞ находим

$\lim_{n \rightarrow ∞}(1-\frac{\lambda}{n})^{n}=e^{–\lambda}$

тогда формула Пуассона примет вид

---

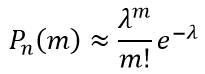
Пример 1
Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятности того, что магазин получит разбитых бутылок:
а) ровно две;
б)  менее двух;
в) более двух;
г) хотя бы одну.
Решение

---

Пример 2
Вероятность выигрыша по одному лотерейному билету р=0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью Р, не меньшей, чем 0,95?
Решение
В этой задачи имеем два противоположных события «ни один из лотерейных билетов не выигрышный» и «хотя бы один лотерейный билет выигрышный», отсюда

P=1–P(0)

Так как

P(0)=λ⁰·e^–λ/0!=e^–λ

P=1–e^–λ

По условию задачи

1–e^–λ≥0.95

e^–λ≤0.05

По таблице  при e^-x=0.05 находим λ=3, так как e^–x убывающая функция, следовательно должно выполняться неравенство λ≥np, тогда подставляя значения в выражения, имеем

 3≥n·0.01

n≥300

Нужно купить не менее 300 билетов, чтобы выиграть хотя бы по одному из лотерейных билетов.

---

Пример 3

Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.

Решение
Здесь, р=0,01, n=200, для вычисления вероятности применим формулу Пуассона, тогда:

   λ=n⋅p=200⋅0.01=2

P₂₀₀(4)=λ⁴⋅e^-λ/4!

   P₂₀₀(4)=2⁴⋅e^-2/4! ≈ 2⋅0.13534≈0.09

---

Пример 4

Вероятность наступления события в каждом из одинаковых независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит ровно 5 раз
Решение
Здесь n — большое значение, р — маленькое значение.
λ = np = 150 ∙ 0,02 = 3, k = 5. 
По формуле Пуассона имеем,
${P_{150}}(5) \approx \frac{{{3^5}{e^{ — 3}}}}{{5!}} \approx 0,1008$
Здесь ещё пример.