Интегральная теорема Муавра – Лапласа

Если число испытаний n→∞ стремится к бесконечности

Вероятность p события не близко к нулю и к единице 0<<p<<1

Тогда из этого следует, что событие наступит не менее k₁ раз и не более k₂ раз.

Формула интегральной функции Лапласа имеет вид:

  

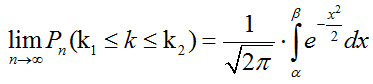
$$P({k_1} \leqslant k \leqslant {k_2}) \approx \Phi (\beta ) — \Phi (\alpha )$$

$$\alpha  = \frac{{{k_1} — np}}{{\sqrt {npq} }}$$

$$\beta  = \frac{{{k_2} — np}}{{\sqrt {npq} }}$$

Ф — функция Лапласа (находится по таблице)

q=1-p

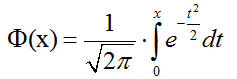
Функция нечетна, т.е.

$$\Phi ( — x) =  — \Phi (x)$$

---

Пример

Вероятность выпуска нестандартного изделия p=0.1. Чему равна вероятность того, что в партии из 1000 изделий число стандартных не менее 890 штук.

Решение

Из условия получаем

p=1-0,1=0,9

q=0.1

n=1000

k₁=1000

k₂=890

Значения Φ находим по таблице Лапласа здесь.