Вероятностью события А называют отношение m на n и определяется по формуле:
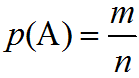
m — числа всех благоприятных комбинаций этому событию исходов эксперимента;
n — общее число всех возможных исходов эксперимента.
Вероятность события А обозначается Р(А).
Основные понятия классической теории вероятности и свойство вероятности рассмотрено здесь.
Рассмотрим примеры, основанные на классическом определение вероятностей.
Пример 1
В урне 10 красных и 8 синих шаров. Наугад вынимают один. Какова вероятность того, что вынут шар красного цвета?
Решение
$p = \frac{{10}}{{18}} = \frac{5}{9}$
Пример 2
В урне 2 белых и 5 черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белым.
Решение
$p = \frac{{2 — 1}}{{2 + 5 — 1}} = \frac{1}{6}$
Пример 3
Игральная кость бросается один раз. Найти вероятность следующих событий:
А1 — появление нечетного числа очков;
A2 — появление не менее 3 очков;
A3 — появление не более 5 очков.
Решение
- Возможные варианты выпадения очков при одном бросании кости: 1, 2, 3, 4, 5, 6. Нечётные — 1, 3, 5. Тогда вероятность равна:
$p({A_1}) = \frac{m}{n} = \frac{3}{6} = \frac{1}{2}$
2. Появление не менее 3 очков — это очки: 3, 4, 5, 6, следовательно
$p({A_2}) = \frac{m}{n} = \frac{4}{6} = \frac{2}{3}$
3. Появление не более 5 очков — это очки: 1, 2, 3, 4, 5, тогда имеем
$p({A_3}) = \frac{m}{n} = \frac{5}{6} $
Пример 4
Монета брошена два раза. Найти вероятность того, что хотя бы один раз появился «герб».
Решение
Найдем все комбинации n подбрасывания монеты два раза, имеем:
«решка» — «герб»
«герб» — «решка»
«решка» — «решка»
«герб» — «герб»
Составим все комбинации события m А — «при бросании монеты два раза хотя бы один раз появился герб»
«решка» — «герб»
«герб» — «решка»
«герб» — «герб»
Тогда
$p({A}) = \frac{m}{n} = \frac{3}{4} $
Пример 5
Бросаются одновременно две игральные кости. Найти вероятности следующих событий:
- А1 — сумма выпавших очков равна 9;
2. A2 — произведение выпавших очков равно 6;
3. A3 — сумма выпавших очков больше 4.
Решение
Составим всевозможные комбинаций, при которых сумма очков двух игральных костей равна 9
| Первая кость | Вторая кость |
| Три | Шесть |
| Шесть | Три |
| Пять | Четыре |
| Четыре | Пять |
Итак, m=4
Общее количество комбинаций равно
n=6·6=36
$p({A_1}) = \frac{m}{n} = \frac{4}{36} = \frac{1}{9}$
2. Составим таблицу, при котором произведение выпавших очков равно 6;
| Первая кость | Вторая кость |
| Три | Два |
| Два | Три |
| Шесть | Один |
| Один | Шесть |
m=4, n=6·6=36
$p({A_2}) = \frac{m}{n} = \frac{4}{36} = \frac{1}{9}$
3. Чтобы найти сумму выпавших очков больше 4, сначала найдём сумму очков, которая меньше 4, для этого составим таблицу
| Первая кость | Вторая кость |
| Один | Два |
| Два | Один |
| Один | Один |
| Два | Два |
| Один | Три |
| Три | Один |
m=36-6=30, n=6·6=36
Найдем событие A3 — сумма выпавших очков больше 4
$p({A_3}) = \frac{m}{n} = \frac{30}{36} = \frac{15}{18} $
Пример 6
В коробке 6 одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Решение
Событие «номера извлеченных кубиков появятся в возрастающем порядке» может произойти в одном случае, то есть m=1.
По формуле комбинаторики перестановка без повторений найдем число комбинаций извлечения шести кубиков
$n = {P_6} = 6! = 1\cdot2\cdot3\cdot4\cdot5\cdot6 = 720$
Вероятность извлеченных кубиков в возрастающем порядке равна:
$P\left( A \right) = \frac{1}{{720}}$
Пример 7
Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры
Решение
А — «абонент набрал нужные три цифры»
m — число благоприятных комбинаций событию А — одно;
n — число комбинаций, которыми можно набрать три цифры и вычисляется по формуле размещение без повторения, тогда
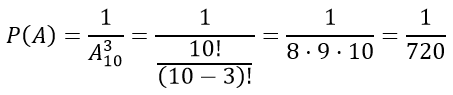
Пример 8
В пачке 20 перфокарт, помеченных номерами 101, 102, … , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
Решение
Событие А — «перфораторщица наудачу извлекает две карты с номерами 101 и 120».
Общее число комбинаций выбора 2-ух карт из 20 равно:
$C_{20}^2 = \frac{{20!}}{{2!\cdot18!}} = \frac{{19\cdot20}}{{1\cdot2}} = 190$
Количество благоприятных комбинаций событию А — одно, получаем
$P\left( A \right) = \frac{1}{{C_{20}^2}} = \frac{1}{{190}}$
Пример 9
В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
Решение
А — «хотя бы одна из взятых деталей окрашена»
Событие A может произойти в трёх случаях:
«одна деталь окрашена», «две детали окрашены», «три детали окрашены»
Противоположное событие $\overline A $ событию A, это «все три детали не окрашены», получаем вероятность
![]()
А противоположное событие исходя из условия задачи находится по формуле
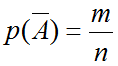
Общее число исходов извлечённых из ящика четыре окрашенных деталей из десяти равно
$m = $C_{6}^4$
Число извлечённых из ящика трех деталей из десяти
$m = $C_{10}^4$
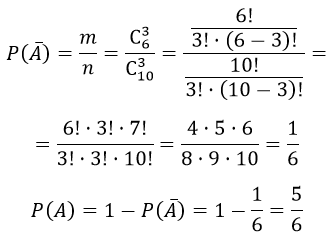
Пример 10
В урне 3 белых и 7 черных. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми.
Решение
Пусть событие A — вероятность того, что оба шара будут белыми.
Найдем общее число случаев по формуле сочетание без повторений
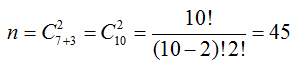
Количество благоприятных случаев выбора двух белых шаров из трёх равно
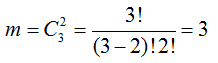
Получаем решение, воспользовавшись общей формулой теории вероятностей
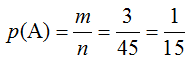
Пример 11
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение
А — «три извлеченные детали сборщиком окажутся окрашенными».
Здесь,
m— количество комбинаций извлечения трех окрашенных деталей из десяти;
n— общее число извлечения трех деталей из пятнадцати.
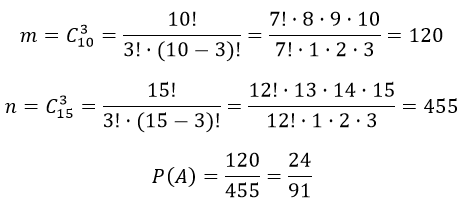
Пример 12
Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
Решение
А — «студент знает предложенные ему экзаменатором три вопроса»
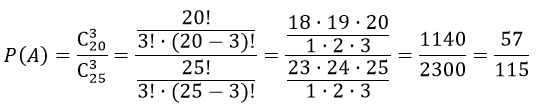
Пример 13
В коробке 5 белых и 7 красных шара. Из нее одновременно наугад вынимают два шара. Найти вероятность того, что они разного цвета.
Решение
$n = C_{7 + 5}^2$
$m = C_5^1 \cdot C_7^1$
Через формулу комбинаторики сочетание без повторений, найдём вероятность вынуть шары разных цветов (один красный и один белый шар), равна
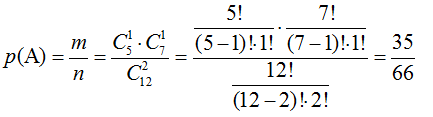
Пример 14
На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода
Решение
А — «из пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода».
Число способов выбрать три кинескопа Львовского завода из десяти кинескопов Львовского завода равно $C_{10}^3$
Число способов выбрать два кинескопа, которые не изготовлены Львовским заводом из пяти равно $C_{5}^2$
Таким образом
$m = C_{10}^3 \cdot C_5^2$
Число комбинаций, которыми можно выбрать пять кинескопов из пятнадцати
$n=C_{15}^5$
Следовательно,
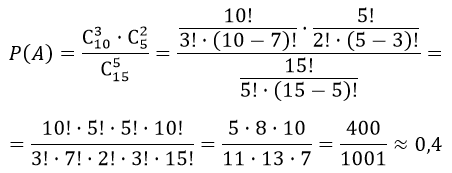
Пример 15
Устройство состоит из пяти элементов, два из которых изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
Решение
$P\left( A \right) = \frac{{C_3^2}}{{C_5^2}} = \frac{3}{{10}} = 0,3$
Пример 16
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся:
1) одно окрашенное изделие;
2) два окрашенных изделия;
3) хотя бы одно окрашенное изделие.
Решение
1) А — «среди двух извлеченных изделий окажется одно окрашенное изделие»
Число способов выбрать одно изделие из трех окрашенных изделий $C_{3}^1$
Неокрашенное изделие можно выбрать $C_{2}^1$
тогда m равно
$m = $C_{3}^1 \cdot C_{2}^1$
Общее число способов, которыми можно выбрать два изделия из пяти равно
$n=C_{5}^2$
Имеем,
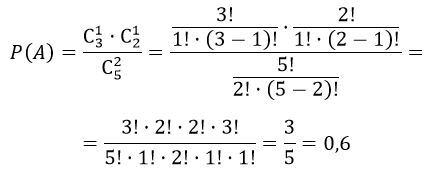
2) В — «два извлеченных изделия окрашены»
Число комбинаций извлечения двух окрашенных изделий $m = $C_{3}^2$
Общее число комбинаций извлечения два изделия из пяти $n=C_{5}^2$
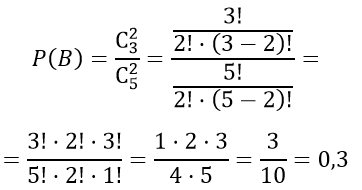
3) С — «извлечено хотя бы одно окрашенное изделие»
Число благоприятных способов извлечения двух изделий нет двух неокрашенных соответствует единице. Тогда:
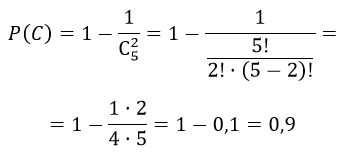

Пример 14 там ошибка в вычислениях
Добрый день! В 14 примере описка, исправили.