Закон распределения дискретной случайной величины можно представить в графическом виде с помощью декартова системой координат, то есть если по оси OY отложить вероятности этих значений pi, a по оси OX значения случайной величины xi и соединив точки между собой получим многоугольником распределения.
Многоугольник распределения является одной из форм закона распределения случайной величины.
Пример
Закон распределения случайной дискретной величины X задан в виде таблицы.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| p | 0.05 | 0.2 | 0.3 | 0.2 | 0.15 | 0.1 |
Требуется построить многоугольник распределения дискретной случайной величины.
Решение
Для построения многоугольник распределения дискретной СВ воспользуемся прямоугольной (декартовой) системой координат и на графике отметим точки в соответствии с таблицей выше:
(0; 0,05), (1; 0,2), (2; 0,3), (3; 0,2), (4; 0,15) и (5; 0,1)
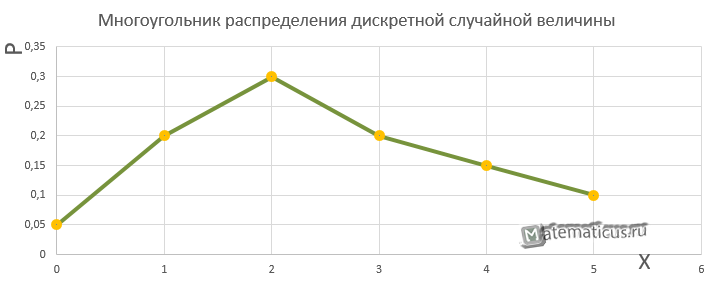
Соединив точки между собой, построим многоугольника распределения дискретной случайной величины

Круто
Согласен!
А ты хорош, только мб уже никогда не увидишь это. А если и увидишь, то я не увижу ответ, уже точно. Если ты конечно захочешь ответить и ответишь соответственно)