Таблица Пирсона

Таблицы

Таблица Пирсона (хи-квадрат) при уровни значимости α=0,05, α=0,01 и т.д.

k $$P({\chi ^2} > \chi _{}^2) = \alpha $$
0,25 0,1 0,05 0,025 0,01 0,005 0,001
1 1,32 2,71 3,84 5,02 6,63 7,88 10,8
2 2,77 4,61 5,99 7,38 9,21 10,6 13,8
3 4,11 6,25 7,81 9,35 11,3 12,8 16,3
4 5,39 7,78 9,49 11,1 13,3 14,9 18,5
5 6,63 9,24 11,1 12,8 15,1 16,7 20,5
6 7,84 10,6 12,6 14,4 16,8 18,5 22,5
7 9,04 12 14,1 16 18,5 20,3 24,3
8 10,2 13,4 15,5 17,5 20,1 22 26,1
9 11,4 14,7 16,9 19 21,7 23,6 27,9
10 12,5 16 18,3 20,5 23,2 25,2 29,6
11 13,7 17,3 19,7 21,9 24,7 26,8 31,3
12 14,8 18,5 21 23,3 26,2 28,3 32,9
13 16 19,8 22,4 24,7 27,7 29,8 34,5
14 17,1 21,1 23,7 26,1 29,1 31,3 36,1
15 18,2 22,3 25 27,5 30,6 32,8 37,7
16 19,4 23,5 26,3 28,8 32 34,3 39,3
17 20,5 24,8 27,6 30,2 33,4 35,7 40,8
18 21,6 26 28,9 31,5 34,8 37,2 42,3
19 22,7 27,2 30,1 32,9 36,2 38,6 43,8
20 23,8 28,4 31,4 34,2 37,6 40 45,3
21 24,9 29,6 32,7 35,5 38,9 41,4 46,8
22 26 30,8 33,9 36,8 40,3 42,8 48,3
23 27,1 32 35,2 38,1 41,6 44,2 49,7
24 28,2 33,2 36,4 39,4 43 45,6 51,2
25 29,3 34,4 37,7 40,6 44,3 46,9 52,6
26 30,4 35,6 38,9 41,9 45,6 48,3 54,1
27 31,5 36,7 40,1 43,2 47 49,6 55,5
28 32,6 37,9 41,3 44,5 48,3 51 56,9
29 33,7 39,1 42,6 45,7 49,6 52,3 58,3
30 34,8 40,3 43,8 47 50,9 53,7 59,7

Значения χ2 критерия Пирсона — таблица

k

$$P({\chi ^2} > \chi _{}^2) = \alpha $$
0,995 0,99 0,975 0,95 0,9 0,75 0,5
1 0,000039 0,00016 0,00098 0,0039 0,016 0,102 0,455
2 0,01 0,02 0,051 0,103 0,211 0,575 1,39
3 0,072 0,115 0,216 0,352 0,584 1,21 2,37
4 0,207 0,297 0,484 0,711 1,06 1,92 3,36
5 0,412 0,554 0,831 1,15 1,61 2,67 4,35
6 0,676 0,872 1,24 1,64 2,2 3,45 5,35
7 0,989 1,24 1,69 2,17 2,83 4,25 6,35
8 1,34 1,65 2,18 2,73 3,49 5,07 7,34
9 1,73 2,09 2,7 3,33 4,17 5,9 8,34
10 2,16 2,56 3,25 3,94 4,87 6,74 9,34
11 2,6 3,05 3,82 4,57 5,58 7,58 10,3
12 3,07 3,57 4,4 5,23 6,3 8,44 11,3
13 3,57 4,11 5,01 5,89 7,04 9,3 12,3
14 4,07 4,66 5,63 6,57 7,79 10,2 13,3
15 4,6 5,23 6,26 7,26 8,55 11 14,3
16 5,14 5,81 6,91 7,96 9,31 11,9 15,3
17 5,7 6,41 7,56 8,67 10,1 12,8 16,3
18 6,26 7,01 8,23 9,39 10,9 13,7 17,3
19 6,84 7,63 8,91 10,1 11,7 14,6 18,3
20 7,43 8,26 9,59 10,9 12,4 15,5 19,3
21 8,03 8,9 10,3 11,6 13,2 16,3 20,3
22 8,64 9,54 11,0 12,3 14,0 17,2 21,3
23 9,26 10,2 11,7 13,1 14,8 18,1 22,3
24 9,89 10,9 12,4 13,8 15,7 19,0 23,3
25 10,5 11,5 13,1 14,6 16,5 19,9 24,3
26 11,2 12,2 13,8 15,4 17,3 20,8 25,3
27 11,8 12,9 14,6 16,2 18,1 21,7 26,3
28 12,5 13,6 15,3 16,9 18,9 22,7 27,3
29 13,1 14,3 16,0 17,7 19,8 23,6 28,3
30 13,8 15 16,8 18,5 20,6 24,5 29,3
k $$P({\chi ^2} > \chi _{}^2) = \alpha $$
0,995 0,99 0,975 0,95 0,9 0,75 0,5
1 0,000039 0,00016 0,00098 0,0039 0,016 0,102 0,455
2 0,01 0,02 0,051 0,103 0,211 0,575 1,39
3 0,072 0,115 0,216 0,352 0,584 1,21 2,37
4 0,207 0,297 0,484 0,711 1,06 1,92 3,36
5 0,412 0,554 0,831 1,15 1,61 2,67 4,35
6 0,676 0,872 1,24 1,64 2,2 3,45 5,35
7 0,989 1,24 1,69 2,17 2,83 4,25 6,35
8 1,34 1,65 2,18 2,73 3,49 5,07 7,34
9 1,73 2,09 2,7 3,33 4,17 5,9 8,34
10 2,16 2,56 3,25 3,94 4,87 6,74 9,34
11 2,6 3,05 3,82 4,57 5,58 7,58 10,3
12 3,07 3,57 4,4 5,23 6,3 8,44 11,3
13 3,57 4,11 5,01 5,89 7,04 9,3 12,3
14 4,07 4,66 5,63 6,57 7,79 10,2 13,3
15 4,6 5,23 6,26 7,26 8,55 11 14,3
16 5,14 5,81 6,91 7,96 9,31 11,9 15,3
17 5,7 6,41 7,56 8,67 10,1 12,8 16,3
18 6,26 7,01 8,23 9,39 10,9 13,7 17,3
19 6,84 7,63 8,91 10,1 11,7 14,6 18,3
20 7,43 8,26 9,59 10,9 12,4 15,5 19,3
21 8,03 8,9 10,3 11,6 13,2 16,3 20,3
22 8,64 9,54 11,0 12,3 14,0 17,2 21,3
23 9,26 10,2 11,7 13,1 14,8 18,1 22,3
24 9,89 10,9 12,4 13,8 15,7 19,0 23,3
25 10,5 11,5 13,1 14,6 16,5 19,9 24,3
26 11,2 12,2 13,8 15,4 17,3 20,8 25,3
27 11,8 12,9 14,6 16,2 18,1 21,7 26,3
28 12,5 13,6 15,3 16,9 18,9 22,7 27,3
29 13,1 14,3 16,0 17,7 19,8 23,6 28,3
30 13,8 15 16,8 18,5 20,6 24,5 29,3

Как пользоваться таблицей Пирсона

k — число степеней свободы, определяется по формуле:

k=n−r−1

где
m — количество признаков; 
r — количество оцениваемых параметров распределения случайной величины.
Для нормального распределения число степеней свободы находится по формуле

k=ι−3

Уровень значимости α берется из условия задачи.
Например α=0,01, k=12, тогда
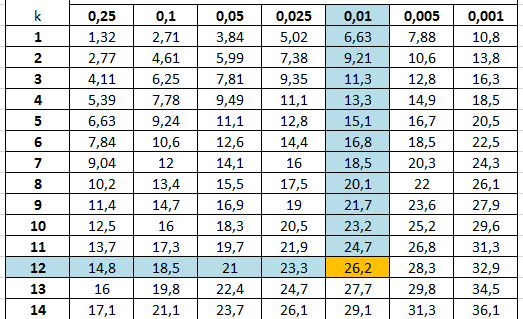
Как пользоваться таблицей Пирсона
Получаем значение Fтабл=26,2

16363

One comment

  1. Здравствуйте!
    Подскажите, из какого источника литературы взята таблица Пирсона (хи-квадрат) при уровни значимости α=0,05, α=0,01 и т.д.

    Ответить

Leave a Reply

Ваш адрес email не будет опубликован.