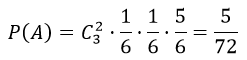Теорема умножения вероятностей независимых событий определяется по формуле:
Р(А·В) = Р(А)·Р(В)
В случае условной вероятности появления события А, формула имеет вид:
Р(А·В) = Р(В)·РВ(А)
Независимые события в совокупности определяются по формуле:
Р(А1·А2·А3·…·Аn) = Р(А1)·Р(А2)·Р(А3)· …·Р(Аn)
Рассмотрим примеры с решением.
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго—0,8. Найти вероятность того, что при одном залпе в мишень попадут оба стрелка.
Решение
А — «первый стрелок попал в мишень»
В — «второй стрелок попал в мишень»
А и В — независимые события
АВ — «оба стрелка попали в мишень».
Р(А·В) = Р(А)·Р(В) = 0,7·0,8 = 0,56
3 стрелка стреляют в мишень. Вероятность попадания в мишень 0.5,0.6,0.7 Происходит залп. Какова вероятность что попадут из них двое, неважно кто.
Решение
А — «двое стрелка попадут в мишень, один промахнется»
По условию p1=0.5; p2=0.6; p3=0.7;
Р(А)=p1·p2·(1-p3)+p1·(1-p2)·p3+(1-p1)·p2·p3=
=0.5·0.6·(1-0.7)+0.5·(1-0.6)·0.7+(1-0.5)·0.6·0.7=0,44
Пример 3
В первой урне имеется 10 черных и 8 белых шара, во второй — 4 черных и 2 белых шара. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара черные?
Решение
А — «из первой урны извлечен черный шар»,
В — «из второй урны извлечен черный шар»,
АВ — «оба шара черные».
$P(A) = \frac{{10}}{{18}} = \frac{5}{9}$
$$P(B) = \frac{4}{6} = \frac{2}{3}$$
$$P(AB) = \frac{5}{9} \cdot \frac{2}{3} = \frac{{10}}{{27}}$$
Пример 4
Из колоды, содержащей 36 карт, наудачу извлекаются три карты. Найдите вероятность того, что все они одной масти
Решение
Пусть событие А — «извлечь подряд из колоды карт три карты одной масти»
Вероятность извлечь одну карту одной масти равна
$P(A_1) = \frac{{9}}{{36}} = \frac{1}{4}$
Вероятность извлечь вторую карту одной масти равна
$P(A_2) = \frac{{8}}{{35}} $
Вероятность извлечь вторую карту одной масти равна
$P(A_3) = \frac{{7}}{{34}} $
По теореме умножения, вероятность подряд извлечь три карты одной масти равна
$P(A) = \frac{{1}}{{4}}\cdot \frac{{8}}{{35}} \cdot \frac{{7}}{{34}}= \frac{1}{85}$
Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится:
а) не более чем в трех ящиках;
б) не менее чем в двух ящиках.
Решение
А1 — «нужная сборщику деталь содержится в первом ящике»
Р(А1) = 0,6
$\overline {{A_1}}$ — «деталь не содержится в первом ящике»
$P(\overline {{A_1}})$=1-Р(А1)=1-0,6=0,4
А2 — «нужная сборщику деталь содержится во втором ящике»
Р(А2)=0,7
$\overline {{A_2}}$ — «деталь не содержится во втором ящике»
$P(\overline {{A_2}})$=1-Р(А2)=1-0,7=0,3
А3 — «нужная сборщику деталь содержится в третьем ящике»
Р(А3)=0,8
$\overline {{A_3}}$ — «деталь не содержится в третьем ящике»
$P(\overline {{A_3}})$=1-Р(А3)=1-0,8=0,2
A4— «нужная сборщику деталь содержится в четвертом ящике»
Р(A4)=0,9
$\overline {{A_4}}$ — «деталь не содержится в четвертом ящике»
$P(\overline {{A_4}})$=1-Р(А4)=1-0,9=0,1
а)
А — «нужная сборщику деталь содержится не более чем в трёх ящиках»
События А1,А2,А3,А4 — независимы, то по теореме умножения имеем:
Р(А)=1-Р(А1)·Р(А2)·Р(А3)·Р(А4)=
=1-0,6·0,7·0,8·0,9=1-0,3024=0,6976
б)
Допустим событие A — «нужная сборщику деталь содержится не менее чем в двух ящиках»
Тогда вероятность этого события равна

Пример 6
В технической системе дублированы не все, а только некоторые (наименее надежные) узлы. Надежности узлов проставлены на рисунке ниже. Определить надежность P системы.
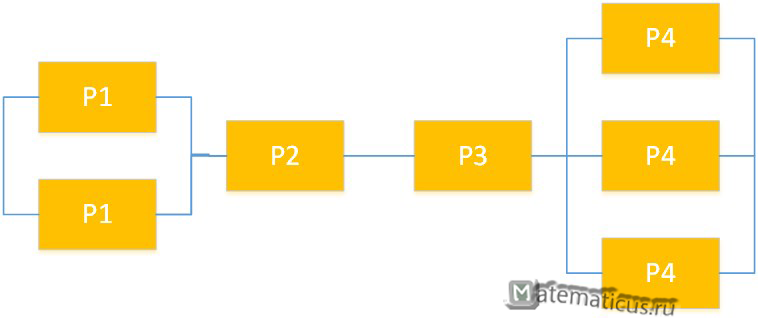
Решение
По теореме умножения получаем
P=[1-(1-p1)2]∙ p2∙ p3∙[1-(1-p4)3]
Брошены три игральные кости. Найти вероятности следующих событий:
а) на каждой из выпавших граней появится пять очков;
б) на всех выпавших гранях появится одинаковое число очков.
Решение
а)
А — «на каждой из выпавших граней пять очков при бросании трех игральных костей»
Вероятность, что на первой игральной кости выпадет пять очков равна
Р(А1)=1/6
Вероятность, что на второй игральной кости выпадет пять очков равна
Р(А1)=1/6
Вероятность, что на третьей игральной кости выпадет пять очков равна
Р(А1)=1/6
События А1, А2, А3 независимы, тогда
P(A)=P(А1)·P(А2)·P(А3)=
=1/6·1/6·1/6=1/216
б)
Допустим событие А — «на каждой из выпавших граней появится одинаковое количество очков при трех бросаниях игральных костей»
В соответствии c пунктом a) и ввиду того, что у кости шесть граней, получаем
P(A)=6·1/6·1/6·1/6=1/36
Пример 8
Брошены три игральные кости. Найти вероятности следующих событий:
а) на двух выпавших гранях появится одно очко, а на третьей грани — другое число очков;
б) на двух выпавших гранях появится одинаковое число очков, а на третьей грани — другое число очков;
в) на всех выпавших гранях появится разное число очков.
Решение
а)
А — «на двух выпавших гранях появится одно очко, а на третьей грани — другое число очков»
$C_3^2$
Вероятность того, что на первой и второй гранях появится одно очко равна 1/6
А вероятность того, что на третий грани появится другой число очков — 5/6
б)
A — «на двух выпавших гранях появится одинаковое число очков, а на третьей грани — другое число очков»
Воспользуемся пунктом a) и то, что у кости шесть граней, имеем:
P(A)=6·P(A)=6·5/72=5/12
в)
A — «на всех выпавших гранях появится разное число очков»
Пусть Р(A1) =1/6, Р(A2)=5/6 (A1≠A2) и Р(A3)=4/6 (A1≠A2≠A3), отсюда по теореме умножения, вероятность равна
P(A)=6·P(A1)·P(A2)·P(A3) =
=6·1/6·5/6·4/6=5/9