Теория игр изучает математические методы оптимальных стратегий применяемых в играх.
Антагонистическая игра или игра с нулевой суммой – это игра, где при любом ходе игроков сумма выигрышей игроков равна сумме всех их проигрышей.
Антагонизм – перев. соперничество.
Конечным случаем в теории игр является игра 2 на 2 и решения матрицы 2×2
| Ai/Bj | B1 | B2 |
| A1 | a11 | a12 |
| A2 | a21 | a22 |
Нижняя цена игры находится по формуле:
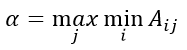
Верхняя цена игры находится по формуле: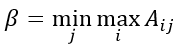
Если α=β, то данная игра имеет седловую точку. Если имеется седловая точка, то оптимальное решение найдено.
Формулы вероятностей (теория игр):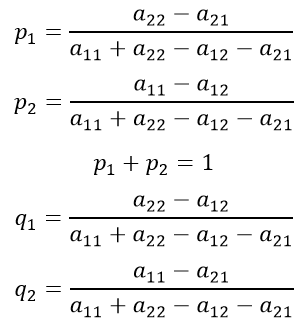
Формула для определения цены игры: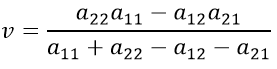
Пример с седловой точкой
Пусть дана платежная таблица игры, найдём оптимальное решение.
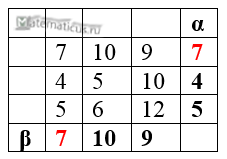
α=max(min(A))=7 – нижняя цена игры
β=min(max(A))=7 – верхняя цена игры
Данная стратегия соответствует седловой точке. Таким образом, так как α=β, то седловая точка равна 7
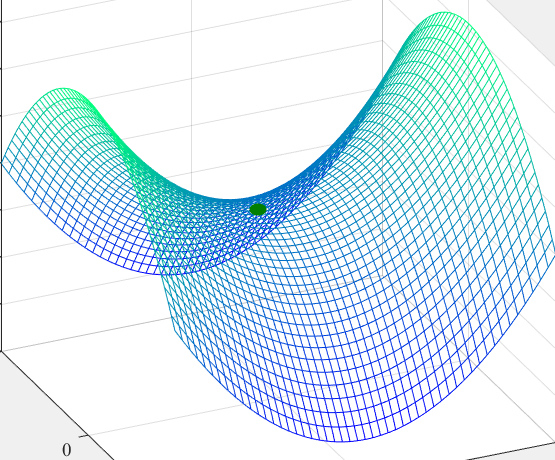
Пример игры 2×2 без седловой точки
Дана платежная таблица
| Ai/Bj | B1 | B2 |
| A1 | 4 | 3 |
| A2 | 2 | 4 |
Найдём нижнюю и верхнюю цену игры
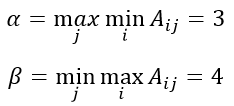
Воспользуемся формулами, получим решение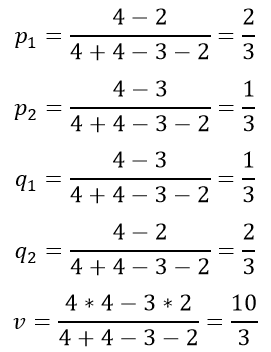
Как упростить платежную матрицу в теории игр см. здесь
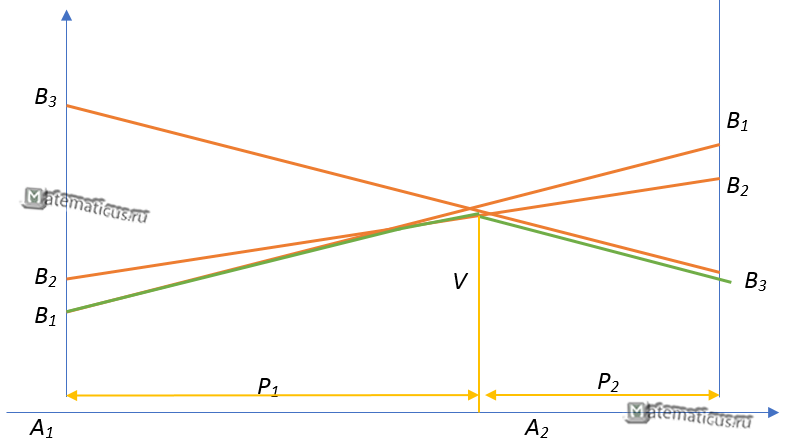
Графически-аналитический или графический способ решения
Пример решение игры 2×n графическим способом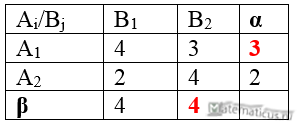
Дана платежная матрица
| Ai/Bj | B1 | B2 | B4 |
| A1 | 3 | 4 | 9 |
| A2 | 8 | 7 | 4 |