Марковская цепь
Цепь Маркова — это математическая модель, которая описывает последовательность случайных событий, где вероятность каждого события зависит только от предыдущего состояния системы.
Свойство Маркова гласит, что вероятность перехода системы из одного состояния в другое зависит только от текущего состояния и не зависит от того, как система пришла в это состояние. Другими словами, будущее состояние системы определяется только текущим состоянием и вероятностями переходов между состояниями.
Распределение вероятностей определяется из выражения:
pi+1=piP2
pi – вектор вероятностей состояний в моменты t=0;
P – матрица вероятностей состояний.
1, 2, 3, 4 – различные состояния объекта (например, 1- исправно работает, 2 – с перебоями, 3 – на ремонте).
Пример
Найти матрицу состояний за два и три шага, распределение вероятностей состояний в моменты t=1 при i=1 и t=2, t=3.
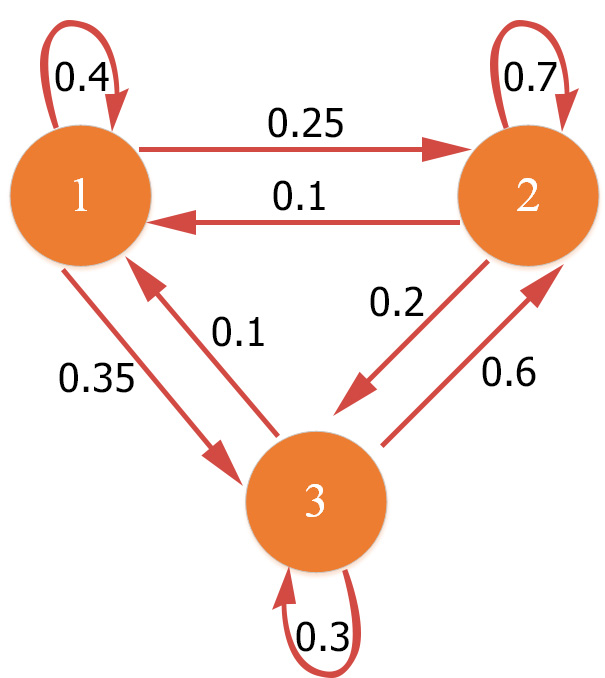
Матрица переходов:

Вектор распределения вероятностей:
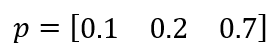
Решение
Найдем матрицу состояний за два шага:

Найдем матрицу состояний за три шага:

Найдем распределение вероятностей состояний в моменты t=1 при i=1

Найдем распределение вероятностей состояний в момент t=2

Найдем распределение вероятностей состояний в момент t=3

