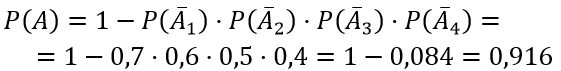Вероятность появления хотя бы одного события

Вероятность наступления события А, заключающийся в появлении хотя бы одного из n независимых в совокупности событий А₁, А₂,…, А_n определяется по формуле:

$P\left( A \right) = 1 — P\left( {\bar A} \right) = 1 — {q_1}\cdot{q_2}\cdot \ldots \cdot{q_n}$

$\overline {{A_1}} ,\overline {{A_2}} , \ldots ,\overline {{A_n}} $  — вероятности противоположных событий.
Вероятность наступления противоположного события $\overline {{A}}$ находится по формуле:

или

q=1–p

где q — вероятность наступления события, противоположного событию A

---

Пример 1
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
q₁ — вероятность неисправности первого платёжного автомата;
q₂ — вероятность неисправности второго платёжного автомата.
Искомая вероятность равна:

P=1–0.02·0.02=0.9996

---

Пример 2

Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.

Решение

А — «стрелки получат приз». Из условия задачи вероятность попадания равна р=0.3, следовательно вероятность их промаха

q=1–р=1–0,3=0,7

Отсюда искомая вероятность равна

  P(A)=1–q⁴=1–0,7⁴=

=1–0,2401=0,7599

---

Пример 3
Вероятность попадания при одном выстреле в мишень 0,7. Найдите вероятность хотя бы одного попадания при 4 выстрелах.
Решение

q=1–р=1–0,7=0,3

P(A)=1–q⁴=1–0,3⁴=

=1–0,0081=0,9919

---

Пример 4
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение
А — «устройство не работает»
A₁ — «отказал первый элемент»
A₂ — «отказал второй элемент»
Найдём вероятности безотказной работы независимых элементов
q₁=1-0,05=0,95,  
q₂=1-0,08=0,92
Следовательно, вероятность того, что устройство не работает равна

 P(A)=1-q₁·q₂=1-0,95·0,92=

==1-0,874=0,126

---

Пример 5
Вероятность того что студент сдаст первый экзамен равна 0.7, второй — 0.5, третий — 0.6. Найти вероятность того, что студентом будет сдан хотя бы один экзамен.
Решение
Здесь событие A — студент сдаст все экзамены
Противоположное событие $\overline {{A}} $ студент не сдаст все экзамены
По теореме умножения имеем

P(A)=1-(1-p₁)·(1-p₂)·(1-p₃)

P(A)=1-(1-0.7)·(1-0.5)·(1-0.6)=0.94

---

Пример 6

Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,5; 0,6

Решение

А — «мост разрушен»

$\overline {{A}}$— «ни одна авиационная бомба не попала в мост»

Здесь события:

A₁=0.3, A₂=0.4, A₃=0.5, A₄=0.6 из условия задачи.
Воспользуемся формулой:

Находим соответствующие им вероятности

$\overline {{A_1}}$ — «первая авиационная бомба не попала в мост »

Р( $\overline {{A_1}}$ ) = 1-0,3 = 0,7

$\overline {{A_2}}$ — «вторая авиационная бомба не попала в мост »

Р($\overline {{A_2}}$) = 1 — 0,4 = 0,6

$\overline {{A_3}}$ — «третья авиационная бомба не попала в мост »

Р($\overline {{A_3}}$) = 1 — 0,5 = 0,5 

$\overline {{A_4}}$ — «четвёртая авиационная бомба не попала в мост »

Р($\overline {{A_4}}$) = 1-0,6 = 0,4

Из условия задачи события  A₁, A₂, A₃ и A₄  независимы, следовательно получаем