Метод Монте-Карло относится к численному стохастическому приближенному математическому методу с использованием датчика случайных чисел. Название метода происходит от казино в Монте-Карло, где случайные числа часто используются в азартных играх.
Основная идея метода Монте-Карло заключается в том, что для оценки сложных математических выражений или моделей можно использовать случайные числа. Путем генерации большого количества случайных выборок и анализа их статистических свойств можно приблизительно решить задачу, которая может быть слишком сложной для точного аналитического решения.
Впервые метод Монте-Карло был применен для приближенного вычисления числа π в задачи Бюффона.
Например, общая формула для определения произвольной площади фигуры S будет иметь вид:
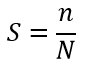
n –количество точек, попавших в область вычисляемой или произвольной фигуры;
N – общее количество точек, N>100.
Точность метода зависит от числа повторений опыта, то есть чем больше количество опытов (повторений), тем выше точность метода.
Рассмотрим метод Моне-Карло на примере вычисления площади круга, находящегося внутри квадрата при этом вероятность выпадение точек на координатной плоскости подчиняется равномерному закону распределения случайной величины.
Для наглядности решение задачи на основе метода Монте-Карло представим в графическом виде.
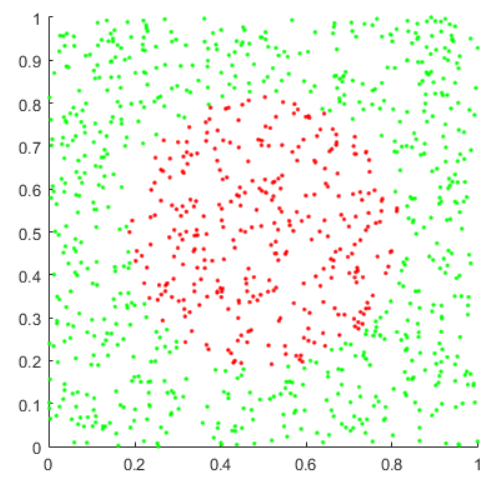
Моделирование с помощью метода Монте Карло при 1000 точек
S=0,322
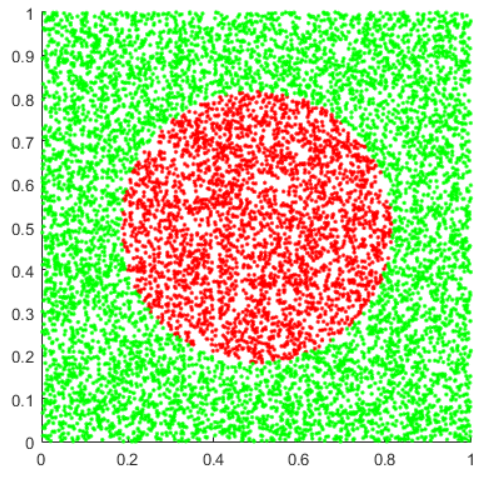
Моделирование с помощью метода Монте Карло при 10000 точек
S=0,3121
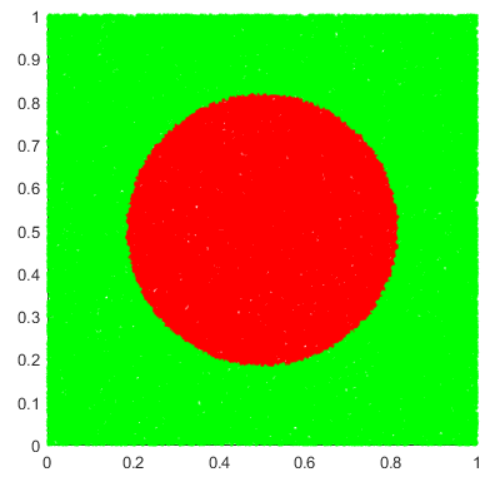
Моделирование с помощью метода Монте Карло при 100000 точек
S=0,31439
Метод применяется для исследования случайных процессов, вычисление площадей фигур (численное интегрирование функций), имитация отжига, математики, физики, экономики и т.д.
