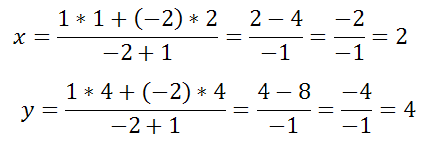пусть даны точки A(x₁;y₁) и B(x₁;y₂), необходимо найти координаты x, y, точки C, делящей отрезок AB в отношении отрезков

   AC:CB=m₁:m₂

взятых именно в этом порядке.

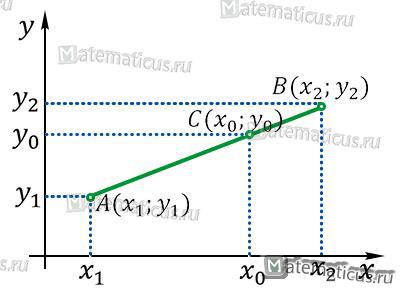
Решение производится формулами

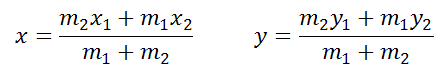
Если отношение m₁:m₂ обозначить буквой λ, тогда формулы примут несимметричный вид.

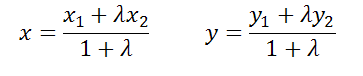Как получаются данные уравнения

Пусть

$\frac{{AC}}{{CB}} = \lambda $

тогда

$\frac{{x — {x_1}}}{{{x_2} — {x_0}}} = \lambda $

 

x-x₁ = λ(x₂-x)

x-x₁ = λx₂-λx

x+λx = x₁+λx₂

получаем уравнение

$x = \frac{{{x_1} + \lambda {x_2}}}{{1 + \lambda }}$

Аналогично выводится и для y

Деление отрезка в данном отношении в пространстве  см. здесь

---

Пример 1
Даны точка С(4;-2) и точка D(-1;5). Найти точку H, делящую CD в отношении 2:3.

Решение
В формулы

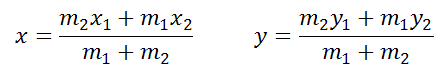
подставляем значения, в соответствии с условием  m₁=2, m₂=3, x₁=4, y₁=-2, x₂=-1, y₂=5

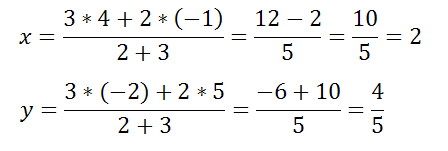
Покажем точку на графике

---

Пример 2
Даны точки A(1;2) и B(4;4). Найти на продолжении отрезка AB точку, стоящую от A вдвое дальше, чем от B.

Решение
Имеем λ=m₁:m₂=-2 (так можно положить, что m₁=-2, m₂=1 или m₁=1, m₂=-2). По формулам

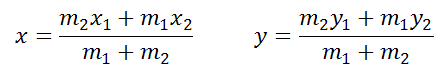
находим: