Как привести уравнение прямой к нормальному виду
Для того, чтобы найти нормальное уравнение прямой, заданной уравнением Ax+By+C=0, необходимо разделить данное уравнение на
при этом знак «минус» берётся, когда C>0, а знак «плюс» берётся, когда C<0. Если C=0, то можно взять любой знак. Тогда получим уравнение вида: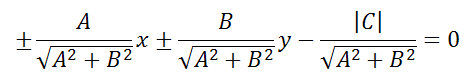 
Если учесть, что полярное расстояние определяется по формуле,
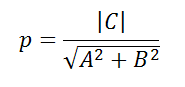
а полярный угол по формулам
Тогда уравнение примет вид
x cosα + y sinα − p = 0
Это и есть нормальное уравнение прямой
То же самое получим, если обе части уравнения Ах + By + С = 0 умножим на число
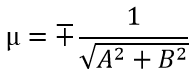
то есть:
x cosα + y sinα − p = 0
Графически это можно представить следующем образом
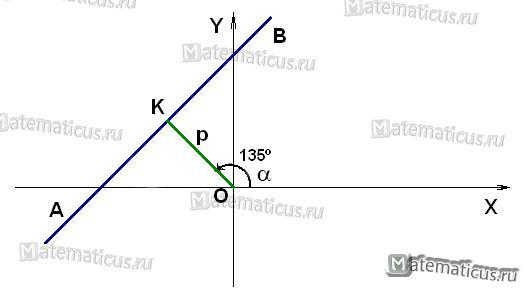
Прямая AB с полярным расстоянием p (длина перпендикуляра, опущенного на прямую из начала координат OK) и полярным углом α (угол измеренный в положительном направлении между положительным направлением оси Ox и направлением этого перпендикуляра) представляется уравнением:
x cosα + y sinα − p = 0
Если p=0, то прямая проходит через начало координат, а угол
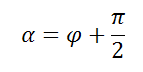
задаёт угол наклона прямой.
Пример 1
Привести уравнение 3x-4y+5=0 к нормальному виду. Здесь A=3, B=-4, C=5>0. Поэтому делим на
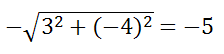получаем
$ — \frac{3}{5}x + \frac{4}{5}x — 1 = 0$
Это уравнение вида
x cosα + y sinα − p = 0
здесь
p=1, $\cos \alpha = — \frac{3}{5}$, $\sin \alpha = \frac{4}{5}$
Пример 2
Пусть прямая AB стоит от начала оси координат на расстоянии OK=$\sqrt 2 $ и пусть луч OK составляет с лучом OX угол равный α=1350
тогда нормальное уравнение прямой AB будет
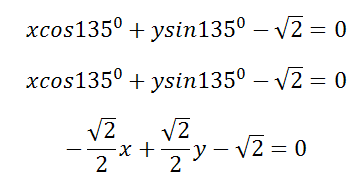
Если умножить полученное уравнение на $-\sqrt 2 $, получим уравнение прямой AB в виде
x-y+2 = 0, но это уравнение не является нормальным уравнением прямой.
3933