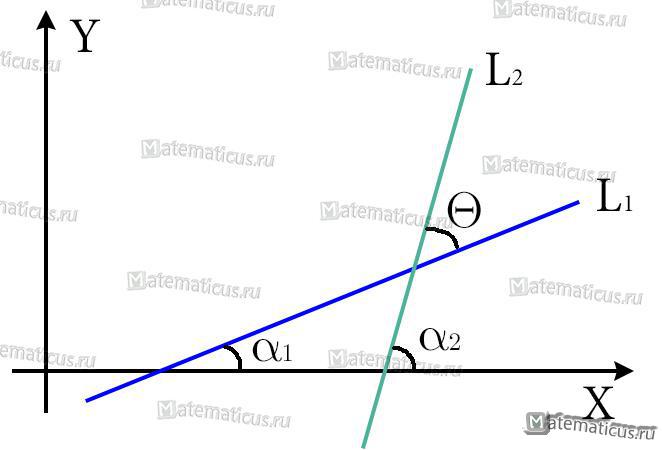
Если две не перпендикулярные прямые, обозначенные как L₁, L₂, представляются уравнениями:

y=k₁x+b₁

y=k₂x+b₂

тогда угол между двумя прямыми находится по формуле:

$\tan \theta  = {\text{tan}}\left( {{\alpha _2} — {\alpha _1}} \right) =$

$\frac{{tan{\alpha _2} — tan{\alpha _1}}}{{1 + tan{\alpha _2}tan{\alpha _1}}} = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}}$

 таким образом, конечная формула угла между двумя прямыми равна:

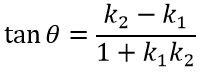
Это выражение даёт угол, на который надо повернуть первую прямую L₁, чтобы она стала параллельной второй прямой L₂

---

Примечание 1
Если хотя бы одна из прямых L₁, L₂ параллельна оси OY, то выше написанная формула неприменима.

В этом случае угол θ определяется следующим образом:

1. Если прямая L₂ параллельна оси OY, а прямая L₁ не параллельна, то применяется формула

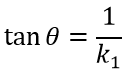
2. Если прямая L₁ параллельно оси OY, а прямая L₂ не параллельна, то применяется формула

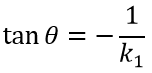
3. Если прямая L₁ и прямая L₂ параллельны оси OY, то они и параллельны друг другом, так что

tgθ = 0

---

Примечание 2
Угол между прямыми, заданными уравнениями

A₁x+B₁y+C1=0 и A₂x+B₂y+C2=0

можно найти по формуле

  
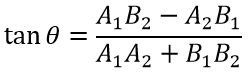
В случае, если A₁A₂+B₁B₂=0, то угол θ=±90 

---

Примечание 3
Если прямые перпендикулярны (θ=±90), то выражение 1+k₁k₂, находящиеся в знаменателе, равно в нулю и тогда θ надо считать равным ±90

---

Пример 1
Найти угол между прямыми y=3x-2 и y=-2x+3.

Решение
Здесь k₁=3, k₂=-2

 $\tan \theta  = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}} =$

$\frac{{ — 2 — 3}}{{1 + 3\cdot\left( { — 2} \right)}} = 1$

Отсюда θ=+45⁰

---

Пример 2
Найти угол между прямыми y=2x−1 и y=−1/2x+5

Решение
Здесь k₁=2, k₂=−1/2   

 $\tan\theta  = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}} = $

$\frac{{ — \frac{1}{2} — 2}}{{1 + \left( { — \frac{1}{2}} \right)\cdot2}} = \frac{{ — 2\frac{1}{2}}}{0}$

Отсюда из примечания 3 следует, что θ=±90⁰

---

Угол между двумя прямыми онлайн калькулятор

---

k₁=

k₂=

---