Указать тип кривой второго порядка

Указать тип кривой второго порядка, найти ее параметры и сделать чертеж

y²=8x+2

Решение задания

y²=8x+2

y²=2·4·(x+$\frac{1}{4}$)

Уравнение можно представить в виде

y²=2·p·x

Полученное уравнение называется каноническим уравнением параболы
где
p — параметр
Так как x=x+$\frac{1}{4}$, следовательно вершина параболы находится в точке ($-\frac{1}{4}$;0)
Отсюда

p=$\frac{8}{2}$=4
F($\frac{7}{4}$;0) — фокус;
x=$-\frac{9}{4}$ — уравнение директрисы;

Ось симметрии y=0

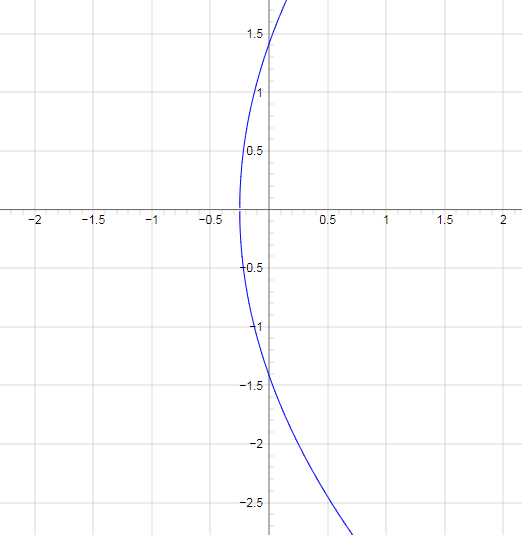
На графике показан чертеж параболы, ветви которой направлены вправо