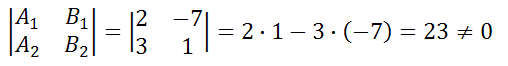Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
y1=k1x+b1
y2=k2x+b2
служит равенство их угловых коэффициентов, то есть
k1=k2
Если прямые заданы уравнениями в общем виде, то есть
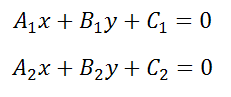
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
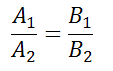
или в другом представлении
![]()
Также это равенство можно записать в виде
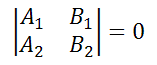
Если свободные члены пропорциональны, то есть,
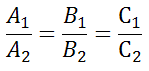
то прямые не только параллельны, но и совпадают.
Пример 1
Уравнения
4x+2y-8=0 и 8x+4y-16=0
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 (на графике синего цвета) и y=4x+7 (прямая красного цвета) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю
$\left| {\begin{array}{*{20}{c}} {{A_1}}&{{B_1}} \\ {{A_2}}&{{B_2}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}} 2&4 \\ 3&6 \end{array}} \right| = 2 \cdot 6 — 3 \cdot 4 = 0$
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю