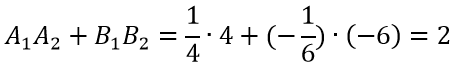Условием перпендикулярности (ортогональности) двух прямых на плоскости, заданных уравнениями:

y₁=k₁x+b₁

y₂=k₂x+b₂ 

служит соотношение

k₁ · k₂  = −1

или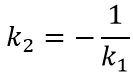

т.е.  угловые коэффициенты k₁, k₂ обратны по величине и противоположны по знаку и это значит, что прямые перпендикулярны, а если произведение угловых коэффициентов не равно -1, то прямые не перпендикулярны.

Если две прямые представлены следующими уравнениями

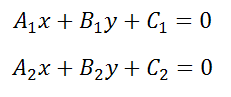
то условием их перпендикулярности (уравнение перпендикулярной прямой) есть

---

Пример 1
Прямые y=4x (прямая синего цвета) и y= -1/4x (прямая красного цвета) перпендикулярны, так как k₁·k₂=4·(-1/4)=-1

---

Пример 2
Прямые 2x+3y=7 и 3x-2y=4 перпендикулярны, так как A₁=2, A₂=3, B₁=3, B₂=-2, следовательно

---

Пример 3
Прямые 1/4x-1/6y=0 и 4x-6y=0 не перпендикулярны, так как здесь