Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
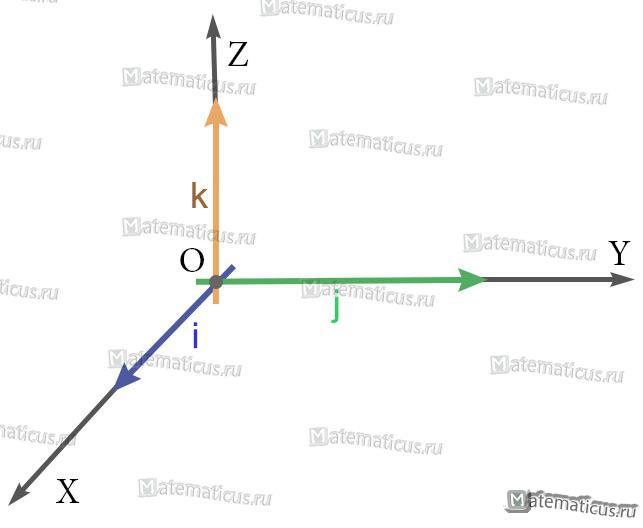
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0);j(0;1;0); k(0;0;1);
Замечание 1
Единичные векторы являются некомпланарными.
Замечание 2
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
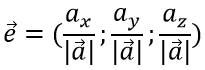
Пример
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Решение
Находим длину вектора a
$\left| {\vec a} \right| = \sqrt {{1^2} + {2^2} + {{\left( { — 2} \right)}^2}} = 3$
затем вычисляем единичный вектор e
$\vec e = \left( {\frac{1}{3};\frac{2}{3}; — \frac{2}{3}} \right)$
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус». Смотрите схему 1.
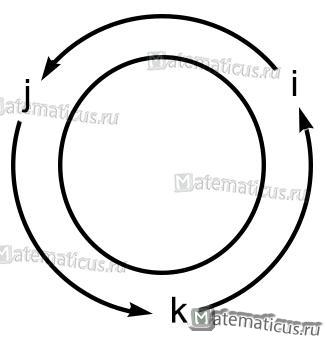
Схема 1
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
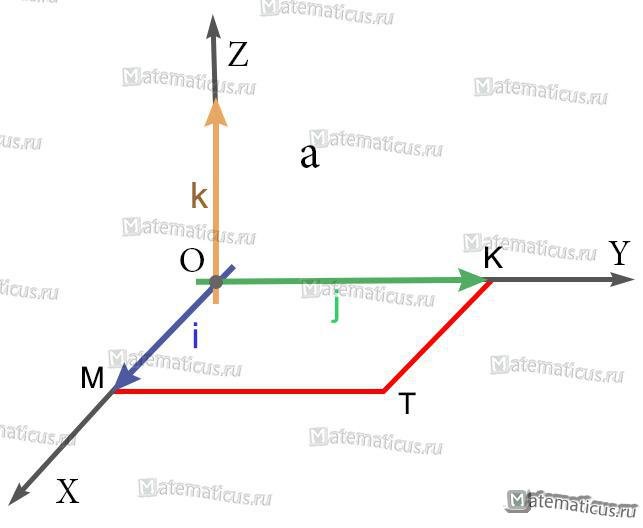
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
