Направляющий вектор прямой

Ненулевой вектор а{l, m, n}, лежащий на прямой KM или параллельный этой прямой называется направляющим вектором.

Координаты l, m, n направляющего вектора называются направляющими коэффициентами прямой. За направляющий вектор прямой KM, образованная  уравнениями двух пересекающихся плоскостей

  A₁x + B₁y + C₁z + D₁=0  (1) 
     A₂x + B₂y + C₂z + D₂=0  (2) 

можно принять векторное произведение N₁×N₂,

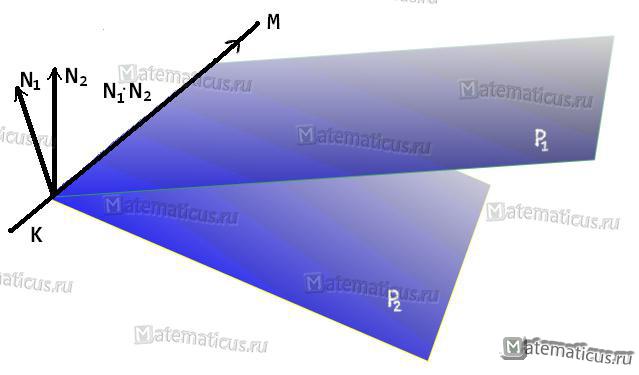
где N₁={А₁, В₁, C₁} и N₂={А₂, В₂, C₂} — нормальные векторы плоскостей Р₁ и Р₂, представляемых уравнениями (1) и (2). На рисунке видно, что прямая KM перпендикулярна к нормальным векторам N₁, N₂

Направляющий вектор можно найти по формуле:

---

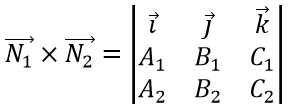
Пример 1

Найти направляющий вектор прямой

2x — y + z + 7=0  (1) 
−3x + 4y + z + 5=0  (2) 

Нормальные векторы имеют координаты N₁={2, -1, 1} и N₂={-3, 4, 1}, подставляя в формулу, получаем

$$\vec N_1 \times \vec N_2 = \left| {\begin{array}{*{20}{c}} {\vec i}&{\vec j}&{\vec k} \\ 2&{ — 1}&1 \\ { — 3}&4&1 \end{array}} \right|=$$

$$=  — 5i — 5j + 5k$$

Следовательно

N₁×N₂=− 5i − 5j + 5k     ⇔    N₁×N₂={−5, −5, 5} 

Это и будет направляющим вектором прямой

---

Пример 2
Найти направляющие коэффициенты прямой

2x-2y-z+5=0, x+2y-2z+3=0

  Решение
Имеем  N₁={А₁, В₁, C₁}, N₂={А₂, В₂, C₂}. Примем а=N₁×N₂, за направляющий вектор данной прямой. Находим:

$$a = \left\{ {\left| {\begin{array}{*{20}{c}} { — 2}&{ — 1} \\  2&{ — 2} \end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ — 1}&2 \\ { — 2}&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}} 2&{ — 2} \\  1&2 \end{array}} \right|} \right\} =$$

$$= \left\{ {6;3;6} \right\}$$

Направляющие коэффициенты будут ι=6, m=3, n=6

Примечание 
Разделив эти числа на 3, найдем направляющие коэффициенты, то есть l’= 2, m’=1, n’=2