Объём треугольной пирамиды, построенной на векторах

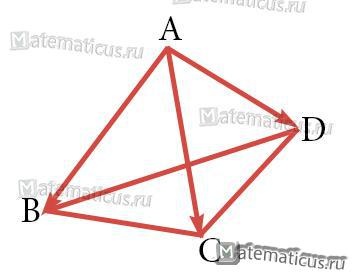
Рисунок — Треугольная пирамида, построенная на векторах

Объём треугольной пирамиды (см. рисунок выше), построенной на векторах вычисляется по формуле:

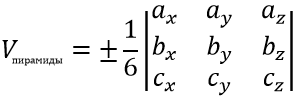
Пример

Найти объём треугольной пирамиды, построенной на векторах ABCD c вершинами

А(2; -1; 1), B(5;5;4), C(3;2;-1), D(4;1;3).

Решение

Находим координаты векторов

$\overrightarrow {AB}  = \left\{ {\left( {5 — 2} \right);\left( {5 — \left( { — 1} \right)} \right);\left( {4 — 1} \right)} \right\} = \left\{ {3;6;3} \right\}$

$\overrightarrow {AC}  = \left\{ {\left( {3 — 2} \right);\left( {2 — \left( { — 1} \right)} \right);\left( { — 1 — 1} \right)} \right\} = \left\{ {1;3; — 2} \right\}$

$\overrightarrow {AD}  = \left\{ {\left( {4 — 2} \right);\left( {1 — \left( { — 1} \right)} \right);\left( {2 — 1} \right)} \right\} = \left\{ {2;2;2} \right\}$

Искомый объём равен $\frac{1}{6}$ объём параллелепипеда, построенного на рёбрах,

$\overrightarrow {AB} $, $\overrightarrow {AС} $, $\overrightarrow {AD} $, следовательно объем равен:

$V =  \pm \frac{1}{6}\left| {\begin{array}{*{20}{c}}3&6&3 \\ 1&3&{ — 2} \\ 2&2&2 \end{array}} \right|=$

$ =  \pm \frac{1}{6}\cdot\left( {3\cdot\left( {3\cdot2 — \left( { — 2} \right)\cdot2} \right) — 6\cdot\left( {1\cdot2 — \left( { — 2} \right)\cdot2} \right) + 3\cdot\left( {1\cdot2 — 3\cdot2} \right)} \right) = 3$

Решая, находим определитель матрицы третьего порядка и получаем искомый объём треугольной пирамиды V=3