Пересечение плоскости с прямой, заданной параметрически

Если существует общая точка плоскости Ax + By + Cz + D=0     (1)
и прямой, заданной параметрическими уравнениями (2)

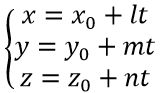
, то пересечение плоскости с прямой находится по формулам (2), если туда подставить значение t, определяемое из уравнения:

  (Аι+Вm+Сn)t+Ах₀+By₀+Cz₀+D=0      

Это уравнение получается, если выражения (2) подставить в (1).

---

Пример 
Найти точку пересечения плоскости x-2y+5z-3=0 с прямой

$\frac{{x — 4}}{2} = \frac{{y — 2}}{{ — 1}} = \frac{{z + 6}}{3}$

  Решение

Параметрические уравнения прямой будут (3):

x=4+2t

y=2-t

z=-6+3t

Подставив в уравнение x-2y+5z-3=0, получим:

4+2t-2⋅(2-t)+5⋅(-6+3t)-3=0
4+2t-4+2t-30+15t-3=0
19t-33=0
$t = \frac{{33}}{{19}}$

Подставляя это значение в уравнение (3), получаем:

 

$x = 4 + 2\cdot\frac{{33}}{{19}}$,

$y = 2 — \frac{{33}}{{19}},$

$x = — 6 + 3\cdot\frac{{33}}{{19}}$

$x = \frac{{142}}{{19}},$

$y = \frac{5}{{19}},$

$x = — \frac{{15}}{{19}}$

Искомая точка есть $\left\{ {\frac{{142}}{{19}};\frac{5}{{19}}; — \frac{{15}}{{19}}} \right\}$