Вектор – направленный отрезок или отрезок, у которого концы упорядочены.
Векторная величина – всякая величина, обладающая направлением.
Скаляр (скалярная величина) – величина, не обладающая направлением.
Пример вектора
Сила, действующая на материальную точку, есть вектор, так как обладает направлением. Например скорость, ускорение, перемещение.
А вот например температура есть скаляр, так как не связано c направлением. Масса, плотность, объём, площадь, время это тоже скаляр.
В аналитической геометрии направленный отрезок называется вектором.
Расстояние между началом и концом вектора называется длиной или модулем вектора. Модуль есть скалярная величина.
О единичном векторе см. здесь
Обозначение вектора
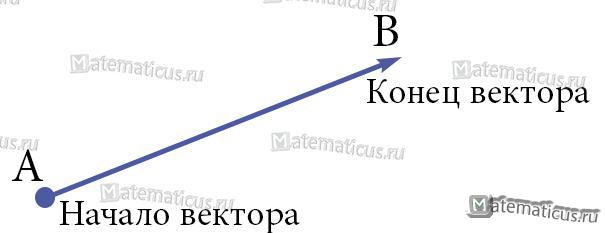
Вектор, началом которого служит A, а концом – B, обозначается , $\overrightarrow {AB} $ также обозначается одной буквой (эту букву печатают жирным шрифтом a, а на письме ставят черту $\left| {\bar a} \right|$).
Модуль вектора обозначается двумя вертикальными чертами слева и справа:
$\overrightarrow {AB} $, или |a| , или $\left| {\bar a} \right|$
Нуль-вектор
Если начало A и конец B отрезка AB совпадают, то отрезок AB обращается в точку и теряет направление. Этот вектор называется нуль-вектором и считается коллинеарным и сонаправленным с любым вектором. Обозначается, как число нуль (знак 0).
Пример
Любая точка пространства может рассматриваться как нуль-вектор.
Коллинеарные векторы
Коллинеарные векторы – это векторы, лежащие на параллельных прямых или лежащие, на одной прямой.
Неколлинеарные векторы – это векторы, не лежащие на параллельных прямых.
Другим словами параллельные вектора называются коллинеарными.
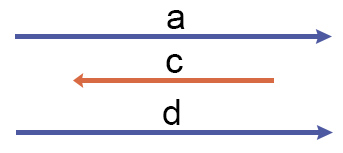
Векторы a, c, d – коллинеарны.
Векторы a и d – векторы имеющие одинаковое направление и их называют или сонаправленными или равнонаправленными векторами, а векторы a и c и векторы с и d называют противоположно направленными.
Компланарные векторы
Компланарными векторами называют три вектора, которые лежат в одной плоскости или (лежат в параллельных плоскостях) параллельны одной плоскости.
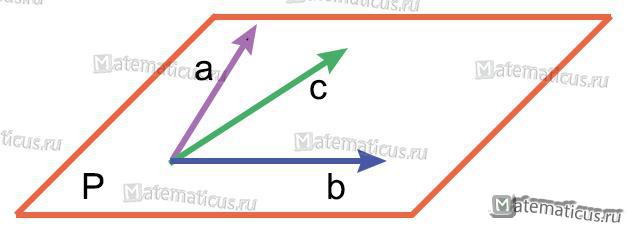
На этом рисунке векторы a,b,c являются компланарными
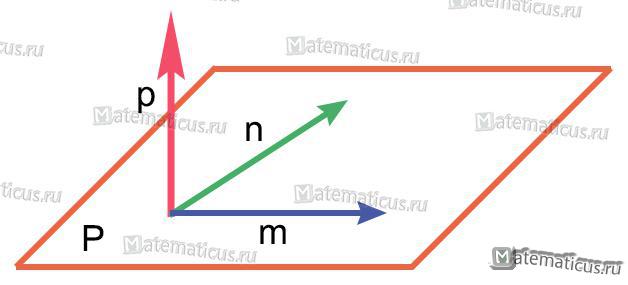
На рисунке векторы m,n,p — некомпланарны
Смешанное произведение трех компланарных векторов равно 0, т.е.
(a, b, c) = 0
Пример смешанного произведения трех компланарных векторов смотрите здесь
Равенство векторов
Два вектора a и b равны, если они равнонаправленные и имеют один и тот же модуль (длину).
Пример 1
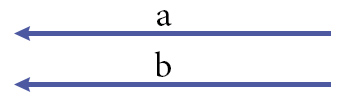
На рисунке векторы a и b равны.
Пример 2
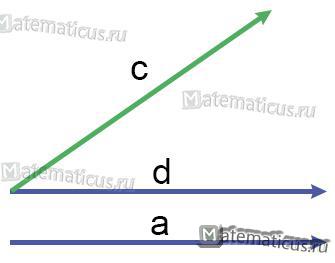
Векторы c и d не равны (даже если длины одинаковы), так как направления различны, следовательно и векторы c и a тоже не равны.
Векторы d и a равны.
Сонаправленные векторы
Сонаправленные векторы — это коллинеарные вектора, направленные в одну сторону, т.е. совпадают направления.
Обозначение: a↑↑b
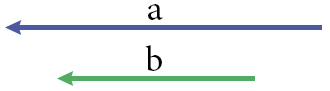
Противоположные векторы
Два коллинеарных (параллельных) вектора, имеющие равные модули и противоположно направленные, т.е. друг другу называются противоположными векторами.
Вектор, противоположный вектору a, обозначается как –a.
Обозначение: a↑↓b
Пример
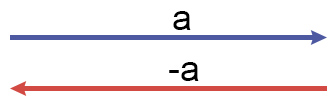
Векторы a и – a — противоположные.
